题目内容
已知三棱锥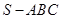 的所有顶点都在球
的所有顶点都在球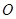 的球面上,
的球面上,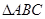 是边长为
是边长为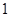 的正三角形,
的正三角形,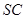 为球
为球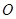 的直径,且
的直径,且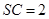 ,则此棱锥的体积为( )
,则此棱锥的体积为( )
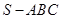 的所有顶点都在球
的所有顶点都在球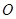 的球面上,
的球面上,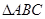 是边长为
是边长为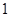 的正三角形,
的正三角形,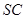 为球
为球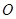 的直径,且
的直径,且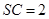 ,则此棱锥的体积为( )
,则此棱锥的体积为( )A.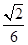 | B.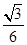 | C.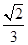 | D.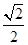 |
A
试题分析:取AB的中点D,连接SD,ED,作SE⊥EC,则AB⊥SD,AB⊥CD,所以AB⊥面SDC,因为
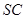 为球
为球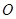 的直径,且
的直径,且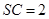 ,所以∠SBAC=∠SAC=900,所以SA=SB=
,所以∠SBAC=∠SAC=900,所以SA=SB=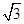 ,所以
,所以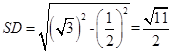 ,
,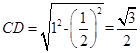 ,在三角形SDC中,
,在三角形SDC中,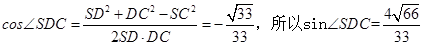 ,
,所以
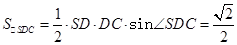 ,所以棱锥的体积
,所以棱锥的体积 。
。点评:求椎体的体积,要适当的选择底面和高。做本题的关键是是把棱锥
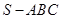 的体积转化为
的体积转化为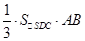 。此题的难度较大。考查了学生分析问题,解决问题的能力。同时也考查了学生的空间想象能力。
。此题的难度较大。考查了学生分析问题,解决问题的能力。同时也考查了学生的空间想象能力。
练习册系列答案
相关题目
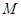 、
、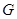 分别是
分别是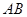 、
、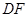 的中点.
的中点.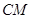
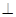 平面
平面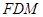
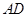 上(含
上(含 、
、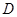 端点)确定一点
端点)确定一点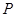 ,使得
,使得
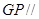 平面
平面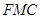 ,并给出证明;
,并给出证明;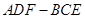 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体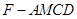 内的概率.
内的概率. 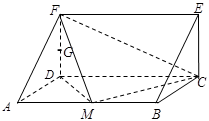
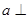 平面
平面 ,直线
,直线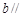 平面
平面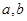 的位置关系是 _
的位置关系是 _ 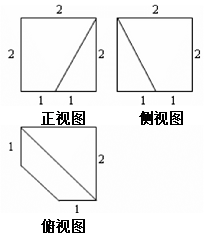






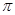


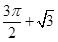
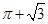

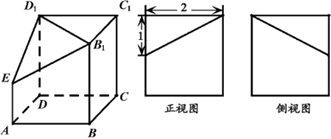
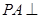 ⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作
⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作 于E,求证:
于E,求证: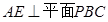 .
. 
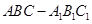 中,已知
中,已知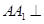 平面ABC,
平面ABC,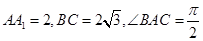 ,且此三棱柱的各顶点都在一个球面上,则球的体积为
,且此三棱柱的各顶点都在一个球面上,则球的体积为 。.
。.