题目内容
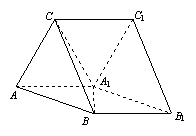 已知三棱柱
已知三棱柱![]() ,侧面
,侧面![]() 侧面
侧面![]() ,
,![]() ,
,![]() 。
。
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平
平
面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
.
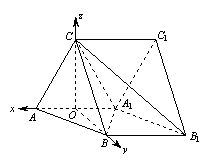 (理)解(1)取
(理)解(1)取![]() 中点O,连接CO,
中点O,连接CO,![]() .
.![]()
![]() ,
,![]() ,
,
又∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() .
.
(2)由(Ⅰ)![]() ,又侧面
,又侧面![]() 侧面
侧面![]() ,侧面
,侧面![]() 侧面
侧面![]() =
=![]()
![]() 平面
平面![]() ,而
,而![]() ,∴
,∴![]() ,
,![]() ,
,![]() 两两垂直.如图,以O为坐标原点,分别以
两两垂直.如图,以O为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系O-xyz.则有
轴建立空间直角坐标系O-xyz.则有
![]() 由对称性知,二面角
由对称性知,二面角![]() 的大小为二面角
的大小为二面角![]() 的两倍
的两倍
设![]() 是平面ABC的一个法向量,K^S*5U.C
是平面ABC的一个法向量,K^S*5U.C
![]()
![]() ,
,
由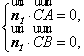 即
即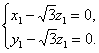 解得
解得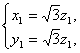 令
令![]() ,∴
,∴![]() .
.
又![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设二面角![]() 为
为![]() ,则
,则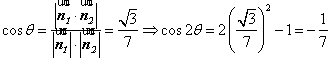 ,
,
所以二面角![]() 的余弦值是
的余弦值是![]() .
.
或:设所求二面角为![]() ,△OBC的BC边上的高为
,△OBC的BC边上的高为![]()
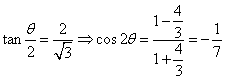
或:![]() 与
与![]() ,BC边上的对应高为二面角的平面角的两夹边(略)
,BC边上的对应高为二面角的平面角的两夹边(略)
(3)假设存在满足条件的点E,∵![]() ,故可设
,故可设![]()
![]() ,
,
则![]() ,
,![]() ,
,![]() ,
, ![]() ,
, ![]()
![]() 平面
平面![]() ,
,![]() ,
,
即![]() ,解得
,解得![]() ,
,![]()

练习册系列答案
相关题目
 (2010•郑州三模)已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
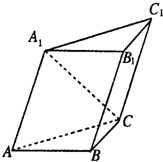
(2010•郑州三模)已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2 如图,已知三棱柱ABC-A1B1C1的侧棱与底面所成的角为60°,AB=BC,A1A=A1C=2,AB⊥BC,侧面AA1C1C⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面所成的角为60°,AB=BC,A1A=A1C=2,AB⊥BC,侧面AA1C1C⊥底面ABC. 的侧面均是矩形,求证:它的任意两个侧面的面积和大于第三个侧面的面积.
的侧面均是矩形,求证:它的任意两个侧面的面积和大于第三个侧面的面积.