题目内容
(2012•湖南)设定义在R上的函数f(x)是最小正周期2π的偶函数,f′(x)是函数f(x)的导函数,当x∈[0,π]时,0<f(x)<1; 当x∈(0,π) 且x≠
时,(x-
)f′(x)>0,则函数y=f(x)-sinx在[-2π,2π]上的零点个数为( )
| π |
| 2 |
| π |
| 2 |
分析:根据x∈(0,π) 且x≠
时,(x-
)f′(x)>0,确定函数的单调性,利用函数的图形,即可得到结论.
| π |
| 2 |
| π |
| 2 |
解答:解:∵x∈(0,π) 且x≠
时,(x-
)f′(x)>0
∴x∈(0,
),函数单调减,x∈(
,π),函数单调增
∵x∈[0,π]时,0<f(x)<1,
在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出y=sinx和y=f(x)草图象如下,
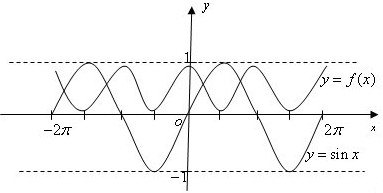
由图知y=f(x)-sinx在[-2π,2π]上的零点个数为4个.
故选B
| π |
| 2 |
| π |
| 2 |
∴x∈(0,
| π |
| 2 |
| π |
| 2 |
∵x∈[0,π]时,0<f(x)<1,
在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出y=sinx和y=f(x)草图象如下,

由图知y=f(x)-sinx在[-2π,2π]上的零点个数为4个.
故选B
点评:本题考查函数的单调性,考查函数的零点,考查函数的周期性与奇偶性,属于基础题.

练习册系列答案
相关题目
