题目内容
已知奇函数y=f(x)在(-∞,0)上为减函数,且f(2)=0,则不等式(x-1)f(x-1)>0的解集为( )
分析:求不等式(x-1)f(x-1)<0的解集,先转化为求不等式xf(x)<0的解集,再由奇函数的图象关于原点对称及f(x)在(-∞,0)为减函数且f(2)=0画出f(x)的草图,即可得到结论.
解答:解:由题意画出f(x)的草图如下,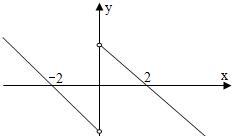
因为(x-1)f(x-1)>0,所以(x-1)与f(x-1)同号,
由图象可得-2<x-1<0或0<x-1<2,
解得-1<x<1或1<x<3,
故选C.

因为(x-1)f(x-1)>0,所以(x-1)与f(x-1)同号,
由图象可得-2<x-1<0或0<x-1<2,
解得-1<x<1或1<x<3,
故选C.
点评:本题考查奇函数的图象特征及数形结合的思想方法,关键是运用转化思想与分类讨论思想,同时作图是该题的突破点,属于基础题.

练习册系列答案
相关题目