题目内容
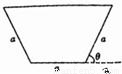
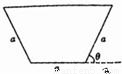
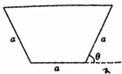 汶川大地震后,为了消除某堰塞湖可能造成的危险,救授指挥部商定,给该堰塞湖挖一个横截面为等腰梯形的简易引水槽(如图所示)进行引流,已知等腰梯形的下底与腰的长度都为a,且水槽的单位时间内的最大流量与横载面的面积为正比,比例系数k>0.
汶川大地震后,为了消除某堰塞湖可能造成的危险,救授指挥部商定,给该堰塞湖挖一个横截面为等腰梯形的简易引水槽(如图所示)进行引流,已知等腰梯形的下底与腰的长度都为a,且水槽的单位时间内的最大流量与横载面的面积为正比,比例系数k>0.(1)试将水槽的最大流量表示成关于θ的函数f(θ);
(2)为确保人民的生命财产安全,请你设计一个方案,使单位时间内水槽的流量最大(即当θ为多大时,单位时间内水槽的流量最大).
分析:(1)利用三角形面积公式表示出水槽的最大流量,注意变量角的取值范围;
(2)利用(1)中的函数式,借助导数知识求出函数的最值,即将设计方案问题转化成最优化问题(最值)解决.
(2)利用(1)中的函数式,借助导数知识求出函数的最值,即将设计方案问题转化成最优化问题(最值)解决.
解答:解:(1)设水槽的横截面面积为s,
则s=
[a+(a+2acosθ)]•asinθ=a2sinθ(1+cosθ).
所以f(θ)=ks=a2ksinθ(1+cosθ),θ∈(0,
).
(2)因为f'(θ)=a2k(2cos2θ+cosθ-1),
令f'(θ)=0,则2cos2θ+cosθ-1=0.
解得cosθ=
或cosθ=-1,
由0<θ<
知cosθ≠-1,所以cosθ=
,θ=
.
当0<θ<
时,f'(θ)>0,即f(θ)在(0,
)上递增,
当
<θ<
时,f'(θ)<0,即f(θ)在(
,
)上递减,
所以当θ=
时,水槽的流量最大,
即设计成θ=
的等腰梯形引水槽,可使单位时间内水槽的流量最大.
则s=
| 1 |
| 2 |

所以f(θ)=ks=a2ksinθ(1+cosθ),θ∈(0,
| π |
| 2 |
(2)因为f'(θ)=a2k(2cos2θ+cosθ-1),
令f'(θ)=0,则2cos2θ+cosθ-1=0.
解得cosθ=
| 1 |
| 2 |
由0<θ<
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
当0<θ<
| π |
| 3 |
| π |
| 3 |
当
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
所以当θ=
| π |
| 3 |
即设计成θ=
| π |
| 3 |
点评:本题主要考查函数在实际生活中的应用、解三角形知识和利用导数求函数最值的方法,解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
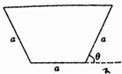 汶川大地震后,为了消除某堰塞湖可能造成的危险,救授指挥部商定,给该堰塞湖挖一个横截面为等腰梯形的简易引水槽(如图所示)进行引流,已知等腰梯形的下底与腰的长度都为a,且水槽的单位时间内的最大流量与横载面的面积为正比,比例系数k>0.
汶川大地震后,为了消除某堰塞湖可能造成的危险,救授指挥部商定,给该堰塞湖挖一个横截面为等腰梯形的简易引水槽(如图所示)进行引流,已知等腰梯形的下底与腰的长度都为a,且水槽的单位时间内的最大流量与横载面的面积为正比,比例系数k>0.