题目内容
设 ,
, ,
, ,
, ,
, 为坐标原点,若
为坐标原点,若 、
、 、
、 三点共线,则
三点共线,则 的最小值是( )
的最小值是( )
 ,
, ,
, ,
, ,
, 为坐标原点,若
为坐标原点,若 、
、 、
、 三点共线,则
三点共线,则 的最小值是( )
的最小值是( )| A.2 | B.4 | C.6 | D. 8 |
D
专题:计算题;不等式的解法及应用.
分析:利用
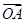 ,
,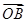 ,
,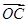 的坐标,结合A,B,C三点共线可求得a,b的关系,利用基本不等式即可求得答案.
的坐标,结合A,B,C三点共线可求得a,b的关系,利用基本不等式即可求得答案.解答:解:∵
 ,
, ,
,
∴
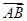 =(a-1,1),
=(a-1,1),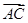 =(-b-1,2),
=(-b-1,2),∵A,B,C三点共线,
∴2(a-1)-(-b-1)=0,
∴2a+b=1.又a>0,b>0,
∴
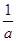 +
+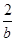 =(
=(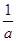 +
+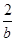 )(2a+b)=2+2+
)(2a+b)=2+2+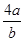 +
+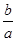 ≥4+2
≥4+2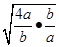 =4+2×2=8(当且仅当a=
=4+2×2=8(当且仅当a=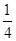 ,b=
,b=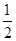 时取等号).
时取等号).故答案为:8.
点评:本题考查向量共线的坐标运算,考查基本不等式,求得是关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

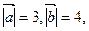 且
且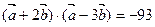 ,求向量
,求向量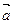 与
与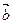 的夹角<
的夹角<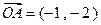 ,
,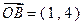 ,
,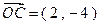 ,在向量
,在向量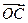 上是否存在点
上是否存在点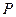 ,使得
,使得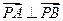 ,若存在,求出点
,若存在,求出点



 ,且
,且 ∥
∥ ,则实数
,则实数 的值等于( )
的值等于( )  或
或

 或
或
 ,
,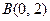 ,点
,点 在单位圆上.
在单位圆上. (
( 为坐标原点),求
为坐标原点),求 与
与 的夹角;
的夹角; ,求点
,求点 的坐标.
的坐标.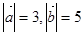 ,如果
,如果 ∥
∥ ,则
,则 = ( )
= ( )



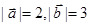 且
且 则
则 的值是( )
的值是( )



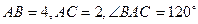 ,点
,点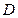 是线段
是线段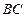 上的动点,则
上的动点,则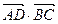 的取值范围是
的取值范围是 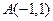 ,
,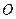 是坐标原点,点
是坐标原点,点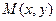 的坐标满足
的坐标满足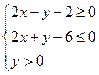 ,则
,则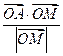 的取值范围是________.
的取值范围是________.