题目内容
若方程x2+ax+b=0有不小于2的实根,则a2+b2的最小值为( )
| A、3 | ||
B、
| ||
C、
| ||
D、
|
分析:本题首先有一个化归问题,把方程x2+ax+b=0看作以(a,b)为动点的直线l:xa+b+x2=0的方程,把代数中的问题转化为解析几何的问题,这是解题的关键,由点到直线的距离d的最小性得到要求的量与已知之间的关系,构造函数,根据函数的单调性解出最值.
解答:解:将方程x2+ax+b=0看作以(a,b)为动点的直线l:xa+b+x2=0的方程,
则a2+b2的几何意义为l上的点(a,b)到原点O(0,0)的距离的平方,
由点到直线的距离d的最小性知a2+b2≥d2
(
)2=
=(x2+1)+
-2(x≥2),
令u=x2+1,易知f(u)=u+
-2(u≥5)在[5,+∞)上单调递增,
则f(u)≥f(5)=
,
∴a2+b2的最小值为
.
故选B.
则a2+b2的几何意义为l上的点(a,b)到原点O(0,0)的距离的平方,
由点到直线的距离d的最小性知a2+b2≥d2
(
| 0+0+x2 | ||
|
| x4 |
| x2+1 |
| 1 |
| x2+1 |
令u=x2+1,易知f(u)=u+
| 1 |
| u |
则f(u)≥f(5)=
| 16 |
| 5 |
∴a2+b2的最小值为
| 16 |
| 5 |
故选B.
点评:本题是一个应用数学中的化归思想来解题的,同时还要用数形结合思想,这是一个综合题,解题过程中用到函数的单调性求最值,是一个中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
下面使用类比推理正确的是( )
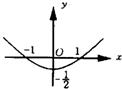
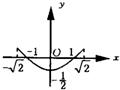
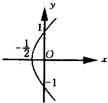
A、直线
| ||||||||||||||||||||||||||||||||||||
| B、同一平面内,直线a,b,c,若a⊥c,b⊥c,则a∥b.类推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b | ||||||||||||||||||||||||||||||||||||
| C、实数a,b,若方程x2+ax+b=0有实数根,则a2≥4b.类推出:复数a,b,若方程x2+ax+b=0有实数根,则a2≥4b | ||||||||||||||||||||||||||||||||||||
| D、以点(0,0)为圆心,r为半径的圆的方程为x2+y2=r2.类推出:以点(0,0,0)为球心,r为半径的球的方程为x2+y2+z2=r2 |



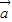 ,
, ,
, ,若
,若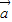 ∥
∥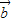 ,
,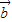 ∥
∥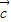 ,则
,则 ∥
∥ .类推出:向量
.类推出:向量 ,
, ,
, ,若
,若 ∥
∥ ,
,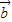 ∥
∥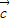 ,则
,则 ∥
∥