题目内容
已知在正项数列{an}中,a1=1,前n项的和Sn满足: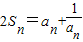 .则此数列的通项公式an= .
.则此数列的通项公式an= .
【答案】分析:根据题目给出的递推式,取n=n+1时得到另外一个式子,两式作差后两边平方运算,得到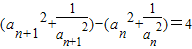 ,构造数列设
,构造数列设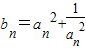 ,则数列{bn}为等差数列,写出等差数列的通项公式,把bn代入后可求an,结合
,则数列{bn}为等差数列,写出等差数列的通项公式,把bn代入后可求an,结合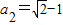 可对求出的an进行取舍.
可对求出的an进行取舍.
解答:解:∵2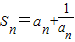 ①
①
∴2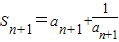 ②
②
②-①得:2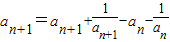 ,
,
所以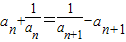 ,
,
两边平方得: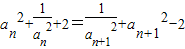 ,
,
即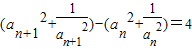
设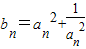 ,则bn+1-bn=4,
,则bn+1-bn=4,
而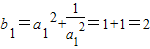 .
.
所以数列{bn}是首项为2,公差为4的等差数列,bn=2+4(n-1)=4n-2.
则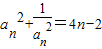 ,即
,即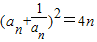 ,又an>0>0,故
,又an>0>0,故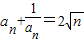 ,
,
从而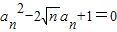 ,解得:
,解得: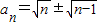 ,
,
而a1=1,由2(a1+a2)=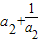 ,即
,即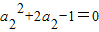 ,解得a2=-1±
,解得a2=-1±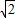 ,
,
取 -1>0,则只有
-1>0,则只有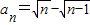 符合.
符合.
所以,此数列的通项公式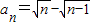 .
.
故答案为有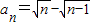 (n∈N*).
(n∈N*).
点评:本题考查了数列的概念及简单表示法,考查了利用递推式求数列的通项公式,在递推式中替换n=n+1(或n-1)得另外一个递推式,两式联立求解是解答此类问题常用的方法,解答该题的关键是两式作差后两边平方,然后构造函数,这也是该题的难点所在,该题是中档题.
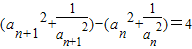 ,构造数列设
,构造数列设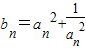 ,则数列{bn}为等差数列,写出等差数列的通项公式,把bn代入后可求an,结合
,则数列{bn}为等差数列,写出等差数列的通项公式,把bn代入后可求an,结合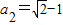 可对求出的an进行取舍.
可对求出的an进行取舍.解答:解:∵2
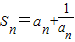 ①
①∴2
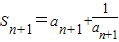 ②
②②-①得:2
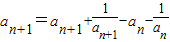 ,
,所以
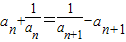 ,
,两边平方得:
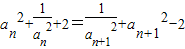 ,
,即
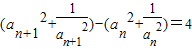
设
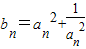 ,则bn+1-bn=4,
,则bn+1-bn=4,而
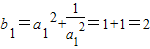 .
.所以数列{bn}是首项为2,公差为4的等差数列,bn=2+4(n-1)=4n-2.
则
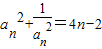 ,即
,即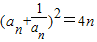 ,又an>0>0,故
,又an>0>0,故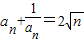 ,
,从而
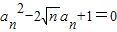 ,解得:
,解得: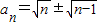 ,
,而a1=1,由2(a1+a2)=
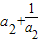 ,即
,即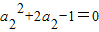 ,解得a2=-1±
,解得a2=-1±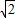 ,
,取
 -1>0,则只有
-1>0,则只有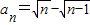 符合.
符合.所以,此数列的通项公式
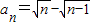 .
.故答案为有
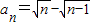 (n∈N*).
(n∈N*).点评:本题考查了数列的概念及简单表示法,考查了利用递推式求数列的通项公式,在递推式中替换n=n+1(或n-1)得另外一个递推式,两式联立求解是解答此类问题常用的方法,解答该题的关键是两式作差后两边平方,然后构造函数,这也是该题的难点所在,该题是中档题.

练习册系列答案
相关题目