题目内容
已知在正项数列{an}中,Sn表示前n项和且2| Sn |
分析:先根据题设条件求得a1,进而根据an=Sn-Sn-1代入且2
=an+1,整理可求得即
-
=1进而判断由定义得{
}是以1为首项,1为公差的等差数列,根据等差数列通项公式求得
=n.则an可得.
| Sn |
| Sn |
| Sn-1 |
| Sn |
| Sn |
解答:解:由已知2
=an+1,得当n=1时,a1=1;
当n≥2时,an=Sn-Sn-1,代入已知有2
=Sn-Sn-1+1,
即Sn-1=(
-1)2.又an>0,
故
=
-1或
=1-
(舍),
即
-
=1(n≥2),
由定义得{
}是以1为首项,1为公差的等差数列,
∴
=n.
故an=2n-1.
| Sn |
当n≥2时,an=Sn-Sn-1,代入已知有2
| Sn |
即Sn-1=(
| Sn |
故
| Sn-1 |
| Sn |
| Sn-1 |
| Sn |
即
| Sn |
| Sn-1 |
由定义得{
| Sn |
∴
| Sn |
故an=2n-1.
点评:本题主要考查了用数列递推式求和通项公式的问题.解题的关键是找到数列中相邻两项或前n项和的相邻两项之间的关系.

练习册系列答案
相关题目
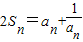 .则此数列的通项公式an= .
.则此数列的通项公式an= .