题目内容
已知在正项数列{an}中，Sn表示前n项和且2
=an+1，则an= ．
| Sn |
分析：将条件平方，再写一式，两式相减，可得数列{an}是以1为首项，2为公差的等差数列，从而可求an．
解答：解：∵2
=an+1，
∴4Sn=(an+1)2，
∴n≥2时，4Sn-1=(an-1+1)2，
两式相减可得4an=(an+1)2-(an-1+1)2，
化简可得（an+an-1）（an-an-1-2）=0，
∵数列各项为正，
∴an-an-1=2，
∵2
=a1+1，
∴a1=1，
∴数列{an}是以1为首项，2为公差的等差数列，
∴an=1+（n-1）×2=2n-1．
故答案为：2n-1．
| Sn |
∴4Sn=(an+1)2，
∴n≥2时，4Sn-1=(an-1+1)2，
两式相减可得4an=(an+1)2-(an-1+1)2，
化简可得（an+an-1）（an-an-1-2）=0，
∵数列各项为正，
∴an-an-1=2，
∵2
| a1 |
∴a1=1，
∴数列{an}是以1为首项，2为公差的等差数列，
∴an=1+（n-1）×2=2n-1．
故答案为：2n-1．
点评：本题考查数列递推式，考查等差数列的判定，考查数列的通项，确定数列{an}是以1为首项，2为公差的等差数列是关键．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
=an+1，求an.
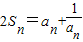．则此数列的通项公式an= ．