题目内容
【题目】如图,四面体![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求四面体![]() 的四个面的面积中,最大的面积是多少?
的四个面的面积中,最大的面积是多少?
(Ⅱ)证明:在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
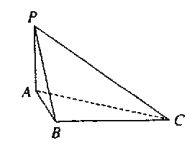
【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】试题分析:(1)易得![]() ,
, ![]() ,
, ![]() ,
, ![]() 均为直角三角形,且
均为直角三角形,且![]() 的面积最大,进而求解即可;
的面积最大,进而求解即可;
(2)在平面ABC内,过点B作BN⊥AC,垂足为N.在平面PAC内,过点N作MN∥PA交PC于点M,连接BM,可证得AC⊥平面MBN,从而使得AC⊥BM,利用相似和平行求解即可.
试题解析:
(1)由题设AB=1,AC=2,BC=![]() ,
,
可得![]() ,所以
,所以![]() ,
,
由PA⊥平面ABC,BC、AB平面ABC,所以![]() ,
, ![]() ,
,
所以![]() ,
,
又由于PA∩AB=A,故BC⊥平面PAB,
PB平面PAB,所以![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() 均为直角三角形,且
均为直角三角形,且![]() 的面积最大,
的面积最大,
![]() .
.
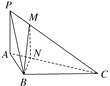
(2)证明:在平面ABC内,过点B作BN⊥AC,垂足为N.在平面PAC内,过点N作MN∥PA交PC于点M,连接BM.
由PA⊥平面ABC知PA⊥AC,所以MN⊥AC.
由于BN∩MN=N,故AC⊥平面MBN.
又BM平面MBN,所以AC⊥BM.
因为![]() 与
与![]() 相似,
相似, ![]() ,
,
从而NC=AC-AN=![]() .
.
由MN∥PA,得![]() =
=![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
