题目内容
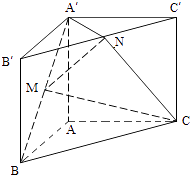
【题目】已知正三棱锥P﹣ABC，点P，A，B，C都在半径为 
的球面上，若PA，PB，PC两两垂直，则球心到截面ABC的距离为 ．
【答案】
【解析】解：∵正三棱锥P﹣ABC，PA，PB，PC两两垂直，
∴此正三棱锥的外接球即以PA，PB，PC为三边的正方体的外接圆O，
∵圆O的半径为 
，
∴正方体的边长为2，即PA=PB=PC=2
球心到截面ABC的距离即正方体中心到截面ABC的距离
设P到截面ABC的距离为h，则正三棱锥P﹣ABC的体积V= 
S△ABC×h= S△PAB×PC= × 
×2×2×2= 
△ABC为边长为2 
的正三角形，S△ABC= 
× 
∴h= 
= 
∴正方体中心O到截面ABC的距离为 ﹣ =
所以答案是
【考点精析】掌握球内接多面体是解答本题的根本，需要知道球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】已知某地每单位面积菜地年平均使用氮肥量x(单位:kg)与每单位面积蔬菜年平均产量Y(单位:t)之间的关系有如下数据:
年份 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
x/kg | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
Y/t | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
x/kg | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
Y/t | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 |
(1)求x与Y之间的相关系数,并检验是否线性相关;
(2)若线性相关,求每单位面积蔬菜年平均产量Y与每单位面积菜地年平均使用氮肥量x之间的回归直线方程,并估计每单位面积菜地年平均使用氮肥150 kg时,每单位面积蔬菜的年平均产量.
