Question

已知点A（2，0），点M为曲线y=

x+2

上任意一点，点P为AM的中点；点P的轨迹为C；
（1）求动点P的轨迹C的方程F（x，y）=0；
（2）将轨迹C的方程变形为函数y=f（x）；请写出此函数的定义域、值域、单调区间、奇偶性、最值等（不证明），并画出大致图象．
（3）若直线l：y=

x

10

+1与轨迹C有两个不同的公共点B，K，且点G的坐标为(

1

8

，0)，求|BG|+|KG|的值．

Answer 1

分析：（1）已知点P为AM的中点，设M（x₁，y₁），P（x，y），由中点坐标公式建立方程，用P点的坐标表示出M点的坐标，再代入书籍的解析式即可求出点P的轨迹为C；
（2）根据函数的解析式写出数的定义域、值域、单调区间、奇偶性、最值等，图象如图；
（3）设B（x₁，y₁），k（x₂，y₂），将直线与轨迹C联立求得有y₁+y₂=5，y₁y₂=5，再由抛物线的性质得到|BG|+|KG|=x1+x2+

1

8

+ 

1

8

=2y1 2+2y2 2+

1

4

=（y₁₊y₂）²-4y₁y₂+

1

4

即可求得|BG|+|KG|的值．

解答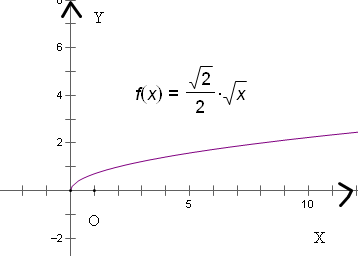：解：（1）已知点P为AM的中点，设M（x₁，y₁），P（x，y）
则

x= x1+2 2 y= y1 2

得

x1=2x-2 y1=2y

∵点M为曲线y=

x+2

上任意一点

y1=

x1+2?

即2y=

2x-2y+2

，即y=

2

2

x

故轨迹C的方程是y=

2

2

x

（2）y=f（x）=

2

2

x

，此函数的性质如下，图象如图；

（3）由直线l与轨迹C相交于B（x₁，y₁），k（x₂，y₂），得

y= 2 2 x y= x 10 +1

，消元得y²-5y+5=0，故有y₁+y₂=5，y₁y₂=5
轨迹C是抛物线y2=

x

2

（y≥0）的一部分，此抛物线的焦点坐标为（

1

8

，0），准线方程为x=-

1

8

所以|BG|+|KG|=x1+x2+

1

8

+ 

1

8

=2y1 2+2y2 2+

1

4

=（y₁₊y₂）²-4y₁y₂+

1

4

=30

1

4

点评：本题考查直线与圆锥曲线的位置关系，解题的关键是根据题设条件灵活选用方法，求得轨迹C的方程，再由其方程对应的曲线的类型选择求值的方法．