题目内容
已知点 的坐标分别是
的坐标分别是 ,直线
,直线 相交于点
相交于点 ,且直线
,且直线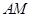 与直线
与直线 的斜率之差是
的斜率之差是 ,则点
,则点 的轨迹方程是( )
的轨迹方程是( )
A. | B. |
C. | D. |
C
解析试题分析:设 ,则
,则 ,化简得
,化简得 。
。
考点:轨迹方程的求法。
点评:求轨迹方程的基本步骤:①建立适当的平面直角坐标系,设P(x,y)是轨迹上的任意一点;②寻找动点P(x,y)所满足的条件;③用坐标(x,y)表示条件,列出方程f(x,y)=0;④化简方程f(x,y)=0为最简形式;⑤证明所得方程即为所求的轨迹方程,注意验证。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
椭圆 的焦距为( )
的焦距为( )
| A. 10 | B. 5 | C. | D. |
已知方程  表示焦点在y轴上的椭圆,则k的取值范围是( )
表示焦点在y轴上的椭圆,则k的取值范围是( )
| A.6<k<9 | B.k>3 | C.k>9 | D.k<3 |
从抛物线 上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦点为F,则△MPF的面积( )
上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦点为F,则△MPF的面积( )
| A.5 | B.10 | C.20 | D. |
若椭圆 的离心率为
的离心率为 ,则双曲线
,则双曲线 的离心率为
的离心率为
A. | B. | C. | D.2 |
抛物线 的准线方程为 ( )
的准线方程为 ( )
A. | B.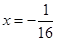 | C. | D. |
 的右焦点作倾斜角为
的右焦点作倾斜角为 的直线
的直线 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则 ( )
( ) C . -3或
C . -3或
 的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q 两点,当四边形PF1QF2面积最大时,
的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q 两点,当四边形PF1QF2面积最大时, 的值等于( )
的值等于( ) 的两焦点为
的两焦点为 ,过
,过 作
作 轴的垂线交双曲线于
轴的垂线交双曲线于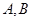 两点,若
两点,若 内切圆的半径为
内切圆的半径为 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )


