题目内容
已知双曲线
的两焦点为
，过
作
轴的垂线交双曲线于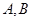
两点，若
内切圆的半径为
，则此双曲线的离心率为（ ）
A． | B． | C． | D． |
D
解析试题分析：由双曲线的定义得：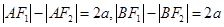
,两式相加得：
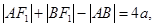又在双曲线中，
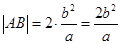，所以
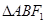的周长为：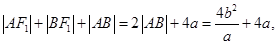
∵内切圆的半径为，∴面积为：
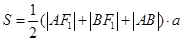，又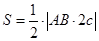
，∴
，
整理得：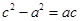
，所以双曲线的离心率为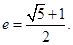
考点：本小题主要考查双曲线的离心率和三角形内切圆的性质.
点评在解题过程中要注意隐含条件的挖掘，注意应用三角形面积的不同计算方法建立关于
的等式求离心率．
练习册系列答案
口算能手系列答案
相关题目
双曲线
的实轴长是虚轴长的2倍，则rn=
A． | B． | C．2 | D．4 |
的左、右焦点，过F1的直线l与C的左、右两支分别交于A，B两点．若｜AB｜：｜BF2｜：｜AF2｜=3：4：5，则双曲线的离心率为
已知点
的坐标分别是
，直线
相交于点
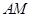，且直线
与直线
的斜率之差是
，则点的轨迹方程是（ ）
A． | B． |
C． | D． |
有一抛物线型拱桥，当水面离拱顶
米时，水面宽
米，则当水面下降
米后，水面宽度为
| A．9 | B．4.5 | C． | D． |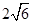
设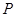
是椭圆
上的点， 
、
是椭圆的两个焦点，则
的值为
| A． 10 | B． 8 | C．6 | D．4 |
已知双曲线
的右焦点为
，则该双曲线的渐近线方程为( )
A． | B． | C． | D． |
下列方程的曲线关于y轴对称的是（ ）
| A．x2－x＋y2＝1 | B．x2y＋xy2＝1 |
| C．x2－y2＝1 | D．x－y="1" |
在椭圆
中，
分别是其左右焦点，若
，则该椭圆离心率的取值范围是 ( )
A． | B． | C． | D． |