题目内容
已知向量a = (1，1)，向量b与向量a 的夹角为
，且a?b = －1.
（1）求向量b；
（2）若向量b与q =（1，0）的夹角为
，向量p = 
，其中A，C为△ABC的内角，且A + C = 
，求|b + p |的最小值.
解：（1）设b=(x,y)， a?b=－1 有x+y=－1 ①
又b与a的夹角为
，所以a?b=| a||b|π，的以x2+y2=1 ②
由①②解得
故b=(－1,0)或b=(－1,0).
（2）由向量b与q垂直知b=（0，－1），由
又因为b+q=
所以|b+q|2=
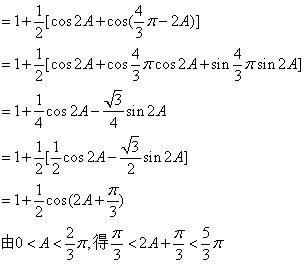
故当
时，|b+p|取得最小值为
练习册系列答案
阅读快车系列答案
相关题目
已知向量
=（1，0），
=（-
，3），则向量
、
的夹角为（ ）
| a |
| b |
| 3 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|