题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
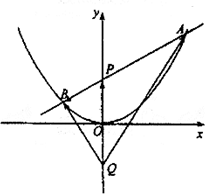
解:依题意,可设直线AB的方程为 代入抛物线方程 设A、B两点的坐标分别是(x1,y1)、(x2,y2),则x1、x2是方程①的两根. 所以
由点P(0,m)分有向线段 得 又点Q是点P关于原点的以称点, 故点Q的坐标是(0,--m),从而
=
= = = =0, 所以 |
(2) |
解:由 由 所以抛物线 设圆C的方程是 则 解之得 所以圆C的方程是 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
| |||||||||||

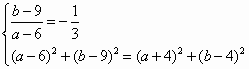 …………………………………………11分
…………………………………………11分