题目内容
已知lga+lgb=0，则函数f（x）=ax与函数g（x）=-logbx的图象可能是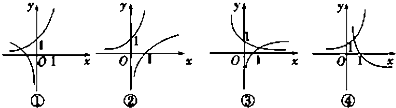
分析：由lga+lgb=0，则得到lgab=0，即ab=1，然后根据指数函数和对数函数的性质即可判断函数的图象．
解答：解：∵lga+lgb=0，
∴lgab=0，即ab=1，
①∵g（x）的定义域为{x|x＞0}，∴①错误．
②由图象知指数函数单调递增，∴a＞1，此时g（x）单调递增，满足条件．
③由图象知指数函数单调递减，∴0＜a＜1，此时g（x）单调递减，不满足条件．
④由图象知指数函数单调递增，∴a＞1，此时g（x）单调递增，不满足条件．
故答案为：②．
∴lgab=0，即ab=1，
①∵g（x）的定义域为{x|x＞0}，∴①错误．
②由图象知指数函数单调递增，∴a＞1，此时g（x）单调递增，满足条件．
③由图象知指数函数单调递减，∴0＜a＜1，此时g（x）单调递减，不满足条件．
④由图象知指数函数单调递增，∴a＞1，此时g（x）单调递增，不满足条件．
故答案为：②．
点评：本题主要考查指数函数和对数函数的图象的判断，利用对数的运算法则确定ab=1是解决本题的关键，根据函数单调性的对应关系解决本题即可．
练习册系列答案
名校课堂系列答案
相关题目
（1）（选修4-4坐标系与参数方程）