题目内容

4．{an}是单调递增的等差数列，前三项的和为12，前三项的积为48，则它的首项是（　　）
A．1B．2C．4D．8

分析 通过记前三项分别为a2-d、a2、a2+d，代入计算即可．

解答 解：由题可知3a2=12，①
（a2-d）a2（a2+d）=48，②
将①代入②得：（4-d）（4+d）=12，
解得：d=2或d=-2（舍），
∴a1=a2-d=4-2=2，
故选：B．

点评 本题考查等差数列的通项公式，注意解题方法的积累，属于基础题．

练习册系列答案
相关题目
14．已知向量$\overrightarrow a$，$\overrightarrow b$满足|$\overrightarrow a$|=3，|$\overrightarrow b$|=2$\sqrt{3}$，且$\overrightarrow a$⊥（$\overrightarrow a$+$\overrightarrow b$），则$\overrightarrow b$在$\overrightarrow a$方向上的投影为-3．
15．$\frac{1+tan15°}{1-tan15°}$的值为（　　）
A．$\frac{\sqrt{3}}{3}$B．$\sqrt{3}$C．2+$\sqrt{3}$D．2-$\sqrt{3}$
12．观察下列不等式：①$\frac{1}{{\sqrt{3}}}$＜1；②$\frac{1}{{\sqrt{3}}}+\frac{1}{{\sqrt{6}}}＜\sqrt{2}$；③$\frac{1}{{\sqrt{3}}}+\frac{1}{{\sqrt{6}}}+\frac{1}{{\sqrt{12}}}＜\sqrt{3}$…，则第5个等式为$\frac{1}{{\sqrt{3}}}+\frac{1}{{\sqrt{6}}}+\frac{1}{{\sqrt{12}}}+\frac{1}{{\sqrt{24}}}+\frac{1}{{\sqrt{48}}}＜\sqrt{5}$．
19．已知α是第一象限角，f（α）=$\frac{sin（π-α）•cos（2π-α）•tan（-α-π）}{tan（-α）•sin（-π-α）}$．
（1）化简f（α）；
（2）若α=-1020°，求f（α）的值．
9．制造容积为$\frac{π}{2}$立方米的无盖圆柱形桶，用来做底面的金属板的价格为每平方米30元，用来做侧面的金属板的价格为每平方米20元，要使用料成本最低，则此圆柱形桶的底面半径和高分别为多少？
16．如果有穷数列a1，a2，a3，…，am（m为正整数）满足条件a1=am，a2=am-1，…，am=a1，即ai=am-i+1（i=1，2，…，m），我们称其为“对称数列”． 例如，数列1，2，5，2，1与数列8，4，2，2，4，8都是“对称数列”． 设{dn}是100项的“对称数列”，其中d51，d52，…，d100是首项为2，公差为3的等差数列．则d2=146；数列{dn}的前n项和Sn=$\left\{\begin{array}{l}{-\frac{3}{2}{n}^{2}+\frac{301}{2}n，}&{1≤n≤50}\\{\frac{3}{2}{n}^{2}-\frac{299}{2}n+7500，}&{51≤n≤100}\end{array}\right.$．
13．有5个球，其中2个一样的黑球，红、白、蓝球各1个，现从中取出4个球排成一列，则所有不同的排法种数是（　　）
A．72B．60C．120D．54
14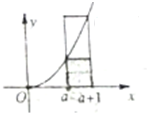．如图，直线x=a，x=a+1（a＞0），y=x2及x轴围成的曲线梯形面积介于相应小矩形与大矩形面积之间，即a2＜${∫}_{a}^{a+1}$x2dx＜（a+1）2．类比之，?n∈N*，$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$＜A＜$\frac{1}{n}+\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立，求实数A等于（　　）
A．$\frac{1}{2}$B．$\frac{3}{5}$C．ln2D．ln$\frac{5}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网