题目内容
证明:如果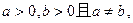 求证:
求证: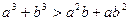
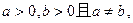 求证:
求证: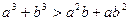
证明:法一:分析法
要证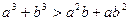
只需证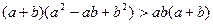 ……2分
……2分
因为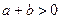 ,要证上式只需证
,要证上式只需证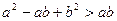 ……4分
……4分
只需证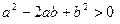 ……6分
……6分
即证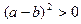 ……8分
……8分
又∵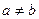 , ∴
, ∴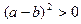 成立 ……10分
成立 ……10分
∴不等式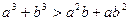 成立 ……12分
成立 ……12分
要证
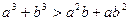
只需证
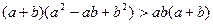 ……2分
……2分因为
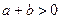 ,要证上式只需证
,要证上式只需证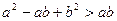 ……4分
……4分只需证
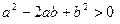 ……6分
……6分即证
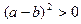 ……8分
……8分又∵
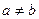 , ∴
, ∴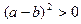 成立 ……10分
成立 ……10分∴不等式
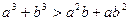 成立 ……12分
成立 ……12分略

练习册系列答案
相关题目
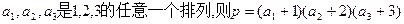 必是偶数.
必是偶数. ,分别求
,分别求 ,
, ,
, ,然后归纳猜想一般性结论,并证明你的结论.
,然后归纳猜想一般性结论,并证明你的结论.
 则此数列中的第
则此数列中的第 项是
项是



 为正整数,用数学归纳法证明
为正整数,用数学归纳法证明
 时,若已假设
时,若已假设 (
( 为偶数)真,则还需利用归纳假设再证( )
为偶数)真,则还需利用归纳假设再证( ) 时等式也成立 B
时等式也成立 B 、
、 时等式也成立
时等式也成立  时等式也成立 D、
时等式也成立 D、 时等式也成立
时等式也成立 都是偶数”,正确的反设为(***)
都是偶数”,正确的反设为(***)