题目内容
若以连续掷两次骰子,分别得到的点数作为点P的坐标,则点P落在圆x2+y2=6内的概率为 .
【答案】分析:由题意知本题是一个等可能事件的概率,试验发生的总事件数是6×6,而点P落在圆x2+y2=6的可以列举出所有的符合条件的事件,得到概率.
解答:解:由题意知是一个等可能事件的概率,
∵由分步计数原理知试验发生的总事件数是6×6,
而点P落在圆x2+y2=6内包括(1,1)(1,2)(2,1)共3种,
由等可能事件的概率公式得到P=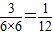
故答案为: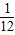
点评:本题主要考查等可能事件的概率,本题解题的关键是看出以掷骰子共有多少中符合题意的结果,本题是一个基础题.
解答:解:由题意知是一个等可能事件的概率,
∵由分步计数原理知试验发生的总事件数是6×6,
而点P落在圆x2+y2=6内包括(1,1)(1,2)(2,1)共3种,
由等可能事件的概率公式得到P=
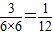
故答案为:
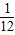
点评:本题主要考查等可能事件的概率,本题解题的关键是看出以掷骰子共有多少中符合题意的结果,本题是一个基础题.

练习册系列答案
相关题目
若以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标,则点P在直线x+y=5下方的概率为.
A、
| ||
B、
| ||
C、
| ||
D、
|
若以连续掷两次骰子(各面分别标有1-6点的正方体)分别得到的点数m、n作为点P的坐标,则点P(m,n)落在区域x2+y2=25内的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|