题目内容
3.画出下列函数图象,并写出函数的单调区间.(1)y=|x2-x-6|;
(2)y=-x2+3|x|+1.
分析 根据函数的解析式画出函数的图象,结合图象读出函数的单调区间即可.
解答 解:(1)y=|x2-x-6|;
画出函数的图象,如图示: ,
,
由图象得:函数在(-∞,-2),($\frac{1}{2}$,3)递减,
在(-2,$\frac{1}{2}$),(3,+∞)递增;
(2)y=-x2+3|x|+1,
x≥0时:y=-x2+3x+1,
x<0时:y=-x2-3x+1,
画出函数的图象,如图示: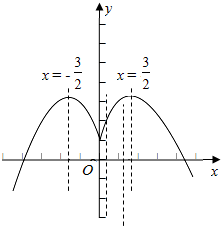 ,
,
由图象得:函数在(-∞,-$\frac{3}{2}$),(0,$\frac{3}{2}$)递增,
在(-$\frac{3}{2}$,0),($\frac{3}{2}$,+∞)递减.
点评 本题考查了二次函数的性质,考查函数的单调性问题,是一道基础题.

练习册系列答案
相关题目
13.直线l:A(x-2)+B(y+3)+C=0交圆M:(x-2)2+(y+3)2=$\frac{4}{3}$于P,Q两点,且A2+B2=3C2,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$=( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{2}{3}$ | C. | -1 | D. | -$\frac{4}{3}$ |
11.一个直角三角形三边的长成等差数列,则下列说法不正确的是( )
| A. | 三边边长之比为3:4:5 | B. | 公差为1或-1 | ||
| C. | 较小锐角的余弦为$\frac{4}{5}$ | D. | 较大锐角的正弦为$\frac{4}{5}$ |
8.已知甲、乙两种食物的维生素A,B含量如表:
设用甲、乙两种食物各xkg,ykg配成至多100kg的混合食物,并使混合食物内至少含有56000单位维生素A和62000单位维生素B,则x,y应满足的所有不等关系为$\left\{\begin{array}{l}{x+y≤100}\\{3x+4y≥280}\\{7x+4y≥620}\\{x≥0,y≥0}\end{array}\right.$.
| 甲 | 乙 | |
| 维生素A(单位/kg) | 600 | 700 |
| 维生素B(单位/kg) | 800 | 400 |