题目内容
已知二次函数f（x）=ax2+bx+c，且函数y=f（x+3）为偶函数，则在函数值f（-1）、f（2）、f（5）、f（7）中，最大的一个不可能是（ ）
分析：根据函数y=f（x+3）为偶函数，它的图象关于y轴对称，而函数f（x）的图象可由函数f（x+3）的图象向右平移三个单位得到，二次函数f（x）关于x=3轴对称，下面对抛物线的开口方向进行分类讨论结合单调性即可得出答案．
解答：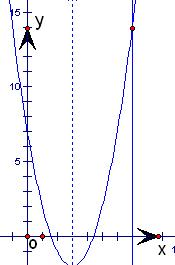
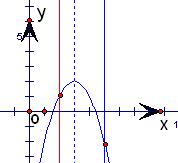解：函数y=f（x+3）为偶函数，
∴它的图象关于y轴对称，
而函数f（x）的图象可由函数f（x+3）的图象向右平移三个单位得到，
∴二次函数f（x）=ax2+bx+c，关于x=3轴对称，
①当a＜0时，则在函数值f（-1）、f（2）、f（5）、f（7）中，最大的一个是f（2）；
②当a＞0时，则在函数值f（-1）、f（2）、f（5）、f（7）中，最大的一个是f（-1）或f（7）；
故选C．
解：函数y=f（x+3）为偶函数，∴它的图象关于y轴对称，
而函数f（x）的图象可由函数f（x+3）的图象向右平移三个单位得到，
∴二次函数f（x）=ax2+bx+c，关于x=3轴对称，
①当a＜0时，则在函数值f（-1）、f（2）、f（5）、f（7）中，最大的一个是f（2）；
②当a＞0时，则在函数值f（-1）、f（2）、f（5）、f（7）中，最大的一个是f（-1）或f（7）；
故选C．
点评：本小题主要考查函数图象的应用、二次函数的性质、函数奇偶性的性质等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目