题目内容
（2011•花都区模拟）如图，平面内有三个向量| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OC |
| OB |
| OC |
| OA |
| OB |
| OC |
| 3 |
| OC |
| OA |
| OB |
分析：过C分别作CN∥OM，交射线OB于N，作CM∥ON，交射线OA于M，先将
写成
+
，再利用向量共线定理求出λ，μ．得出结果．
| OC |
| OM |
| ON |
解答：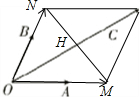
解：过C分别作CN∥OM，交射线OB于N，作CM∥ON，交射线OA于M，
则
=
+
=λ
+μ
．
∴
=λ
=μ
．
由已知，|
|=|
|=1，
平行四边形OMCN中，∠MOC=∠NOC=∠NCO=30°，
∴△NOC为等腰三角形．
∴ON=NC=OM①
∴平行四边形OMCN为菱形．
连接MN交OC于H，则OC⊥MN，且H为OC中点．
在RT△OHM中，cos∠HOM=
=
即cos30°=
=
，解得OM=2，
由①，ON=OM=2．
∴λ=
=2，同理求得μ=2，λ+μ=4
故选A．
解：过C分别作CN∥OM，交射线OB于N，作CM∥ON，交射线OA于M，则
| OC |
| OM |
| ON |
| OA |
| OB |
∴
| OM |
| OA |
| ON |
| OB |
由已知，|
| OA |
| OB |
平行四边形OMCN中，∠MOC=∠NOC=∠NCO=30°，
∴△NOC为等腰三角形．
∴ON=NC=OM①
∴平行四边形OMCN为菱形．
连接MN交OC于H，则OC⊥MN，且H为OC中点．
在RT△OHM中，cos∠HOM=
| OH |
| OM |
| ||
| OM |
即cos30°=
| ||
| OM |
| ||
| 2 |
由①，ON=OM=2．
∴λ=
|
| ||
|
|
故选A．
点评：本题考查空间向量基本定理，向量共线定理的应用．考查转化、计算、解三角形的能力．
练习册系列答案
相关题目
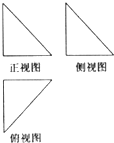（2011•花都区模拟）如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为2，那么 这个几何体的体积为（ ）