题目内容
某学校设计了一个实验学科的考查方案:考生从6道备选题中一次性抽取3道题,规定至少正确完成其中2道题便可通过,已知6道备选题中考生甲有4道能正确完成,2道不能完成;考生乙正确完成每道题的概率都是
,且每题正确完成与否互不影响.
(1)求甲正确完成的题数ξ的分布列及期望;求乙正确完成的题数η的分布列及期望;
(2)请用统计知识分析比较两名考生这门学科的水平.
| 2 | 3 |
(1)求甲正确完成的题数ξ的分布列及期望;求乙正确完成的题数η的分布列及期望;
(2)请用统计知识分析比较两名考生这门学科的水平.
分析:(1)随机变量ξ的所有可能值为1,2,3,且P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
,由此能求出ξ的分布列和E(ξ).
(2)变量η的所有可能值为0,1,2,3,且P(η=k)=
(
)k•(
)3-k,D(ξ)=(2-1)2×
+(2-2) 2×
+(2-3)2×
=
,D(η)=(2-0)2×
+(2-1)2×
+(2-2)2×
+(2-3)2×
=
,所以,从统计的角度可以判断考生甲这门学科的水平更好.
| ||||
|
| 1 |
| 5 |
| ||||
|
| 3 |
| 5 |
| ||||
|
| 1 |
| 5 |
(2)变量η的所有可能值为0,1,2,3,且P(η=k)=
| C | k 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 27 |
| 6 |
| 27 |
| 12 |
| 27 |
| 8 |
| 27 |
| 2 |
| 3 |
解答:解:(1)随机变量ξ的所有可能值为1,2,3,
且P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,
所以ξ的分布列为
所以E(ξ)=1×
+2×
+3×
=2.
随机变量η的所有可能值为0,1,2,3,且P(η=k)=
(
)k•(
)3-k,k=0,1,2,3,
所以P(η=0)=
(
)0(
)3=
,
P(η=1)=
(
)1(
)2=
,
P(η=2)=
(
)2(
)1=
,
P(η=3)=
(
)3(
)0=
,
∴η的分布列为
所以E(η)=0×
+1×
+2×
+3×
=2.
(2)由于随机变量ξ,η的期望相同,所以考虑随机变量ξ,η的方差,
D(ξ)=(2-1)2×
+(2-2) 2×
+(2-3)2×
=
,
D(η)=(2-0)2×
+(2-1)2×
+(2-2)2×
+(2-3)2×
=
,
∴D(ξ)<D(η),所以,从统计的角度可以判断考生甲这门学科的水平更好.
且P(ξ=1)=
| ||||
|
| 1 |
| 5 |
P(ξ=2)=
| ||||
|
| 3 |
| 5 |
P(ξ=3)=
| ||||
|
| 1 |
| 5 |
所以ξ的分布列为
| ξ | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
随机变量η的所有可能值为0,1,2,3,且P(η=k)=
| C | k 3 |
| 2 |
| 3 |
| 1 |
| 3 |
所以P(η=0)=
| C | 0 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
P(η=1)=
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 6 |
| 27 |
P(η=2)=
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 12 |
| 27 |
P(η=3)=
| C | 3 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
∴η的分布列为
| η | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 27 |
| 6 |
| 27 |
| 12 |
| 27 |
| 8 |
| 27 |
(2)由于随机变量ξ,η的期望相同,所以考虑随机变量ξ,η的方差,
D(ξ)=(2-1)2×
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
D(η)=(2-0)2×
| 1 |
| 27 |
| 6 |
| 27 |
| 12 |
| 27 |
| 8 |
| 27 |
| 2 |
| 3 |
∴D(ξ)<D(η),所以,从统计的角度可以判断考生甲这门学科的水平更好.
点评:本题考查离散型随机变量的数学期望和方差的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
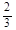 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.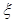 的分布列及期望;求乙正确完成的题数
的分布列及期望;求乙正确完成的题数 的分布列及期望;
的分布列及期望; ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.