题目内容
6.集合A={x|x2-ax+a2-13=0},B={x|x2-5x+4=0},C={x|x2+2x-3=0},求当a取什么实数时,A∩B=∅和A∩C≠∅同时成立.分析 化简B={1,4},C={-3,1},从而可得1,4∉A,-3∈A;从而可得9+3a+a2-13=0,从而解得.
解答 解:B={x|x2-5x+4=0}={1,4},
C={x|x2+2x-3=0}={-3,1},
∵A∩B=∅和A∩C≠∅同时成立,
∴1,4∉A,-3∈A;
∴9+3a+a2-13=0,
故a=-4或a=1;
当a=-4时,A={-1,-3},成立;
当a=1时,A={4,-3},不成立;
故a=-4.
点评 本题考查了集合的化简与元素与集合的关系应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
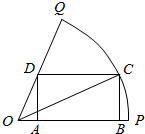 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.