题目内容
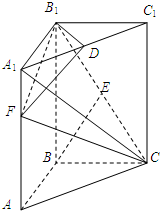 (2008•南京模拟)如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.
(2008•南京模拟)如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.(1)求直线BE与A1C所成的角的余弦;
(2)在线段AA1上取一点F,问AF为何值时,CF⊥平面B1DF?
分析:(1)以B点为原点,BA、BC、BB1分别为x、y、z轴建立空间直角坐标系,用坐标表示点,进而可表示向量,利用向量的数量积可求直线BE与A1C所成的角的余弦;
(2)要使得CF⊥平面B1DF,只需CF⊥B1F,由
•
=0可建立方程,从而得解.
(2)要使得CF⊥平面B1DF,只需CF⊥B1F,由
| CF1 |
| B1F |
解答:解:(1)因为直三棱柱ABC-A1B1C1中,BB1⊥面ABC,∠ABC=
.
以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系,…(2分)
因为AC=2,∠ABC=90°,所以AB=BC=
,
从而B(0,0,0),A(
,0,0),C(0,
,0),
B1(0,0,3),A1(
,0,3),C1(0,
,3),D(
,
,3),E(0,
,
).
所以
=(
,-
,3),
=(0,
,
)
而|
|=
,|
|=
,且
•
=
所以cosθ=
=
=
…(5分)
所以直线BE与A1C所成的角的余弦为
.…(6分)
(2)设AF=x,则F(
,0,x),
=(
,-
,x),
=(
,0,x-3),
=(
,
,0),…(8分)
•
=
×
+(-
)×
+x×0=0,
所以
⊥
,…(9分)
要使得CF⊥平面B1DF,只需CF⊥B1F,由
•
=2+x(x-3)=0,有x=1或x=2,…(11分)
故当AF=1,或AF=21时,CF⊥平面B1DF.…(12分)
| π |
| 2 |
以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系,…(2分)
因为AC=2,∠ABC=90°,所以AB=BC=
| 2 |
从而B(0,0,0),A(
| 2 |
| 2 |
B1(0,0,3),A1(
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
所以
| CA1 |
| 2 |
| 2 |
| BE |
| ||
| 2 |
| 3 |
| 2 |
而|
| CA1 |
| 13 |
| BE |
| ||
| 2 |
| CA1 |
| BE |
| 7 |
| 2 |
所以cosθ=
| ||||
|
|
| ||||||
|
7
| ||
| 143 |
所以直线BE与A1C所成的角的余弦为
7
| ||
| 143 |
(2)设AF=x,则F(
| 2 |
| CF |
| 2 |
| 2 |
| B1F |
| 2 |
| B1D |
| ||
| 2 |
| ||
| 2 |
| CF |
| B1D |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
所以
| CF |
| B1D |
要使得CF⊥平面B1DF,只需CF⊥B1F,由
| CF1 |
| B1F |
故当AF=1,或AF=21时,CF⊥平面B1DF.…(12分)
点评:本题的考点是用空间向量求直线间的夹角与距离,主要考查线线角及线面垂直问题,关键是构建空间直角坐标系,利用向量的数量积求解.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
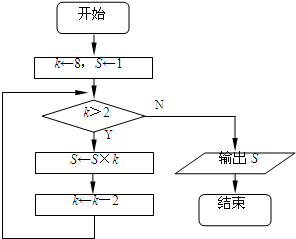 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是