题目内容
13．已知$\frac{1}{2}$＜x＜5是不等式2x2+mx+5＜0的解，则m的取值范围是m≤-9．分析 利用一元二次函数图象分析不等式在定区间上恒成立的条件，再求解即可
解答 解：设f（x）=2x2+mx+5，
∵$\frac{1}{2}$＜x＜5是不等式2x2+mx+5＜0的解，
∴$\left\{\begin{array}{l}{f（\frac{1}{2}）≤0}\\{f（5）≤0}\end{array}\right.$，即$\left\{\begin{array}{l}{\frac{1}{2}+\frac{1}{2}m+5≤0}\\{50+5m+5≤0}\end{array}\right.$，
解得m≤-9
故答案为：m≤-9．
点评 本题考查不等式在定区间上的恒成立问题．利用一元二次函数图象分析求解是解决此类问题的常用方法．
练习册系列答案
小学课时特训系列答案
相关题目
6．
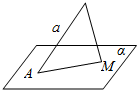已知AB是面α的斜线段，斜足为A，AB=a，点M是面α内的动点，△ABM的面积为定值b，则点M的轨迹是（ ）
已知AB是面α的斜线段，斜足为A，AB=a，点M是面α内的动点，△ABM的面积为定值b，则点M的轨迹是（ ）| A． | 线段 | B． | 椭圆 | C． | 双曲线 | D． | 抛物线 |
5．已知f（x）在定义域（-4，1）上是减函数，且f（1+a）＜f（3a-1），则a的取值范围是（ ）
| A． | （-∞，1） | B． | （-1，0） | C． | （-1，1） | D． | （0，1） |
1．集合A={a，b}，其中非空真子集个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
18．已知函数y=f（x）的图象如图，那么f（x）的表达式为（ ）
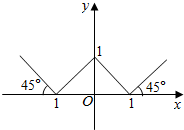
| A． | $\sqrt{{x}^{2}-2x+1}$ | B． | $\sqrt{{x}^{2}-2|x|+1}$ | C． | |x2-1| | D． | -2|x|+1 |
5．函数f（x）=2x2-3|x|的递减区间是（ ）
| A． | [$\frac{3}{4}$，+∞） | B． | （-∞，-$\frac{3}{4}$] | C． | [-$\frac{3}{4}$，0]和[$\frac{3}{4}$，+∞） | D． | （-∞，-$\frac{3}{4}$]，[0，$\frac{3}{4}$] |