题目内容
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=CC1,M,N分别为A1B,B1C1的中点.
(1)求证:MN∥平面ACC1A1;
(2)求证:MN⊥平面A1BC.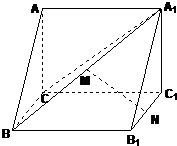
(1)求证:MN∥平面ACC1A1;
(2)求证:MN⊥平面A1BC.

证明:(1)连接AB1,则点M是AB1的中点,又点N是B1C1的中点,
则MN是△AB1C1的中位线,所以MN∥AC1,
根据线面平行的判定得:
MN∥平面ACC1A1;
(2)由BC⊥AC,BC⊥CC11,则BC⊥平面ACC1A1,
连接AC1,则BC⊥AC1.
∵侧面ACC1A1是正方形,所以A1C⊥AC1.
又BC∩A1C=C,根据线面垂直的判定定理可知AC1⊥平面A1BC,
又因为MN∥AC1,
根据线面垂直的性质定理得:
MN⊥平面A1BC;
则MN是△AB1C1的中位线,所以MN∥AC1,
根据线面平行的判定得:
MN∥平面ACC1A1;
(2)由BC⊥AC,BC⊥CC11,则BC⊥平面ACC1A1,
连接AC1,则BC⊥AC1.
∵侧面ACC1A1是正方形,所以A1C⊥AC1.
又BC∩A1C=C,根据线面垂直的判定定理可知AC1⊥平面A1BC,
又因为MN∥AC1,
根据线面垂直的性质定理得:
MN⊥平面A1BC;

练习册系列答案
相关题目




