题目内容
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f![]() (x)g(x)+f(x)g
(x)g(x)+f(x)g![]() (x)<0且f(﹣1)=0则不等式f(x)g(x)<0的解集为( )
(x)<0且f(﹣1)=0则不等式f(x)g(x)<0的解集为( )
A.(﹣1,0)∪(1,+∞)B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)
【答案】A
【解析】
构造函数h(x)=f(x)g(x),由已知得当x<0时,h![]() (x)<0,所以函数y=h(x)在(﹣∞,0)单调递减,又因为f(x),g(x)分别是定义在R上的奇函数和偶函数,得函数y=h(x)为R上的奇函数,所以函数y=h(x)在(0,+∞)单调递减,得到f(x)g(x)<0不等式的解集.
(x)<0,所以函数y=h(x)在(﹣∞,0)单调递减,又因为f(x),g(x)分别是定义在R上的奇函数和偶函数,得函数y=h(x)为R上的奇函数,所以函数y=h(x)在(0,+∞)单调递减,得到f(x)g(x)<0不等式的解集.
设h(x)=f(x)g(x),因为当x<0时,f![]() (x)g(x)+f(x)g
(x)g(x)+f(x)g![]() (x)<0,
(x)<0,
所以当x<0时,h![]() (x)<0,所以函数y=h(x)在(﹣∞,0)单调递减,
(x)<0,所以函数y=h(x)在(﹣∞,0)单调递减,
又因为f(x),g(x)分别是定义在R上的奇函数和偶函数,
所以函数y=h(x)为R上的奇函数,所以函数y=h(x)在(0,+∞)单调递减,
因为f(﹣1)=0,所以函数y=h(x)的大致图象如下:
所以等式f(x)g(x)<0的解集为(﹣1,0)∪(1,+∞)
故选A.
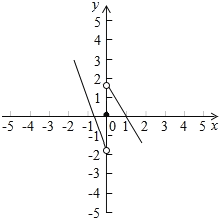

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


