Question

【题目】请你设计一个包装盒，是边长为的正方形硬纸片（如图1所示），切去阴影部分所示的四个全等的等腰三角形，再沿虚线折起，使得，，，四个点重合于图2中的点，正好形成一个正四棱锥形状的包装盒（如图2所示），设正四棱锥的底面边长为.

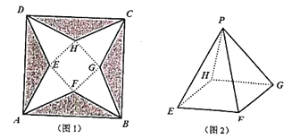
（1）若要求包装盒侧面积不小于，求的取值范围；

（2）若要求包装盒容积最大，试问应取何值？并求出此时包装盒的容积.

Answer 1

【答案】（1）（2）当时，包装盒容积最大为

【解析】

（1）结合已知可建立侧面积关于的函数关系，然后由侧面积不小于，可建立关于的不等式，即可求得的取值范围；
（2）先利用表示出的函数关系，结合导数可求其最大值．

（1）在图1中连结，交于点，设与交于点，在图2中连结，

因为是边长为的正方形，所以，

由，得，，

因为，即，所以.

因为，

由，得，所以.

答：的取值范围是.

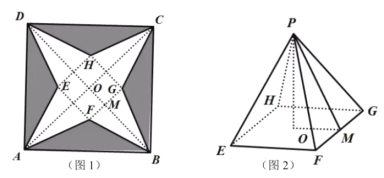
（2）因为在中，，

所以，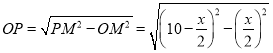

，，

设，，

所以，

令，得或（舍去）.

列表得，

		8
	+	0	-
		极大值

所以当时，函数取得极大值，也是最大值，

所以当时，的最大值为.

答：当时，包装盒容积最大为.