题目内容
用|S|表示集合S中的元素的个数,设A、B、C为集合,称(A,B,C)为有序三元组.如果集合A、B、C满足|A∩B|=|B∩C|=|C∩A|=1,且A∩B∩C=∅,则称有序三元组(A,B,C)为最小相交.由集合{1,2,3}的子集构成的所有有序三元组中,最小相交的有序三元组的个数为 .
分析:根据定义,确定 满足条件的集合A,B,C的元素情况即可求出结果.
解答:解:∵|A∩B|=|B∩C|=|C∩A|=1,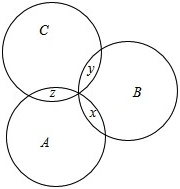
∴设A∩B={x},B∩C={y},C∩A={z},
∵A∩B∩C=∅,且x,y,z∈{1,2,3},
∴集合A,B,C中都只有一个元素.
将1,2,3进行全排列,由
=3×2=6个.
故答案为:6.

∴设A∩B={x},B∩C={y},C∩A={z},
∵A∩B∩C=∅,且x,y,z∈{1,2,3},
∴集合A,B,C中都只有一个元素.
将1,2,3进行全排列,由
| A | 3 3 |
故答案为:6.
点评:本题主要考查集合的关系的应用,正确理解新定义是解决本题关键,利用排列组合的知识是解决本题的突破点.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
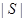 表示集合S中的元素的个数,设
表示集合S中的元素的个数,设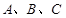 为集合,称
为集合,称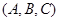 为有序三元组.如果集合
为有序三元组.如果集合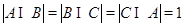 ,且
,且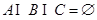 ,则称有序三元组
,则称有序三元组 的子集构成的所有有序三元组中,最小相交的有序三元组的个数为
.
的子集构成的所有有序三元组中,最小相交的有序三元组的个数为
.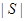 表示集合S中的元素的个数,设
表示集合S中的元素的个数,设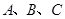 为集合,称
为集合,称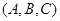 为有序三元组.如果集合
为有序三元组.如果集合 ,且
,且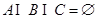 ,则称有序三元组
,则称有序三元组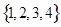 的子集构成的所有有序三元组中,最小相交的有序三元组的个数为
.
的子集构成的所有有序三元组中,最小相交的有序三元组的个数为
.