题目内容
用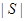 表示集合S中的元素的个数,设
表示集合S中的元素的个数,设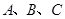 为集合,称
为集合,称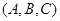 为有序三元组.如果集合
为有序三元组.如果集合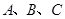 满足
满足 ,且
,且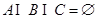 ,则称有序三元组
,则称有序三元组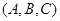 为最小相交.由集合
为最小相交.由集合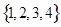 的子集构成的所有有序三元组中,最小相交的有序三元组的个数为
.
的子集构成的所有有序三元组中,最小相交的有序三元组的个数为
.
【答案】
96
【解析】
试题分析: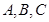 三个集合不可能有一元集,否则不能满足
三个集合不可能有一元集,否则不能满足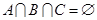 ,又因为
,又因为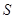 中只有4个元素,则
中只有4个元素,则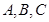 中不可能有两个集合都有3个元素,否则不能满足
中不可能有两个集合都有3个元素,否则不能满足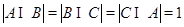 ,但
,但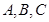 中可以三个集合都含有2个元素,也可能是一个集合有3个元素,其它两个集合含有2个元素,情形如下:
中可以三个集合都含有2个元素,也可能是一个集合有3个元素,其它两个集合含有2个元素,情形如下:
如三个集合都含有2个元素这种情形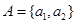 ,
,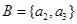 ,
,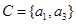 ,这种类型有
,这种类型有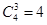 种可能,另外第4个元素
种可能,另外第4个元素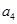 可任意加入上述4种可能中的每一个集合,又形成不同的情形,这样就又有
可任意加入上述4种可能中的每一个集合,又形成不同的情形,这样就又有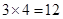 种,于是就共有了
种,于是就共有了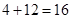 种情形,在每一种情形
种情形,在每一种情形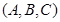 中,它们的顺序可以打乱,每种可形成
中,它们的顺序可以打乱,每种可形成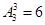 个,因此共有
个,因此共有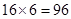 个有序三元组.
个有序三元组.
考点:集合的交集.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目



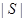 表示集合S中的元素的个数,设
表示集合S中的元素的个数,设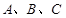 为集合,称
为集合,称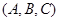 为有序三元组.如果集合
为有序三元组.如果集合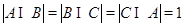 ,且
,且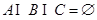 ,则称有序三元组
,则称有序三元组 的子集构成的所有有序三元组中,最小相交的有序三元组的个数为
.
的子集构成的所有有序三元组中,最小相交的有序三元组的个数为
.