题目内容
设{an}是集合{2s+2t|0≤s<t,且s,t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12…,将数列{an}中各项按照上小下大,左小右大的原则排成如下等腰直角三角形数表:
3
5 6
9 10 12
…
则第四行四个数分别为 ;且a2012= (用2s+2t形式表示).
3
5 6
9 10 12
…
则第四行四个数分别为
分析:根据题意,可归纳出第i行的i个数是20+2i,21+2i,22+2i,…,2i-1+2i,由此即可给出出第四行四个数.再由等差数列求和公式,得出a2012是第63行的第59个数,结合前面总结出的规律则不难得到a2012的表达式.
解答:解:由3=20+21,
5=20+22,6=21+22,
9=20+23,10=21+23,3=22+23,
…
可得第i行的i个数是20+2i,21+2i,22+2i,…,2i-1+2i,(i∈N*)
由此可得第四行四个数:20+24=17,21+24=18,22+24=20,23+24=24,
设a2012在第k行,解不等式1+2+3+…+k≥2012
即
k(k+1)≥2012,得满足条件的最小正整数k=63
∴a2012在第63行,
由
×62×63+1=1954,得第63行第一个数为a1954,
∵2012=1954+58,∴a2012=258+263
故答案为:17,18,20,24;258+263
5=20+22,6=21+22,
9=20+23,10=21+23,3=22+23,
…
可得第i行的i个数是20+2i,21+2i,22+2i,…,2i-1+2i,(i∈N*)
由此可得第四行四个数:20+24=17,21+24=18,22+24=20,23+24=24,
设a2012在第k行,解不等式1+2+3+…+k≥2012
即
| 1 |
| 2 |
∴a2012在第63行,
由
| 1 |
| 2 |
∵2012=1954+58,∴a2012=258+263
故答案为:17,18,20,24;258+263
点评:本题给出三角形数阵,要求我们找出其中的规律并给出a2012的表达式,着重考查了等差数列的通项与求和、数列的函数特性等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
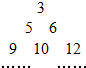 设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表:
设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表: 设{an}是集合{2t+2s|0≤s<t,且s,t∈z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…将数列{an}各项按照上小下大,左小右大的原则写成如图的三角形数表:
设{an}是集合{2t+2s|0≤s<t,且s,t∈z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…将数列{an}各项按照上小下大,左小右大的原则写成如图的三角形数表: