题目内容
若曲线 在点
在点 处的切线与两个坐标围成的三角形的面积为18,则
处的切线与两个坐标围成的三角形的面积为18,则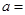 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
A
解析试题分析:因为 ,所以
,所以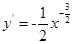 ,所以
,所以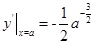 ,所以曲线
,所以曲线 在点
在点 处的切线为
处的切线为 ,当
,当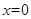 时,
时,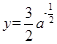 ;当
;当 ,所以切线与两个坐标围成的三角形的面积
,所以切线与两个坐标围成的三角形的面积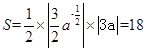 ,所以
,所以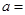 64.
64.
考点:导数的几何意义;直线方程的点斜式;导数的运算法则。
点评:我们要灵活应用导数的几何意义求曲线的切线方程,尤其要注意切点这个特殊点,充分利用切点即在曲线方程上,又在切线方程上,切点处的导数等于切线的斜率这些条件列出方程组求解。属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一个物体的运动方程是s=1+t+t2,其中s的单位是米,t的单位是秒,那么该物体在3秒末的瞬间速度是
| A.6米/秒 | B.7米/秒 | C.8米/秒 | D.9米/秒 |
若 ,则
,则 ( )
( )
A. | B.2 | C. | D. |
若对可导函数 ,恒有
,恒有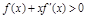 ,则
,则 ( )
( )
| A.恒大于0 | B.恒小于0 |
| C.恒等于0 | D.和0的大小关系不确定 |
已知函数 在
在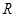 上可导,且
上可导,且 ,则
,则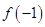 与
与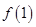 的大小关系为( )
的大小关系为( )
A. | B. | C. | D.不确定 |
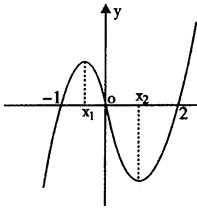
如下图是函数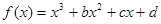 的大致图象,则
的大致图象,则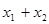 = ( )
= ( )
A.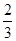 | B.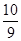 | C.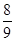 | D.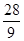 |
曲线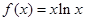 在点
在点 处的切线方程为( )
处的切线方程为( )
A.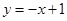 | B. | C. | D.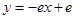 |
函数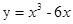 的极大值为( )
的极大值为( )
A.4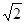 | B.3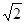 | C.-3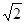 | D.-4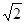 |
 ,且函数
,且函数 在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,则
在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,则 的取值范围为( )
的取值范围为( )


