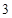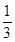题目内容
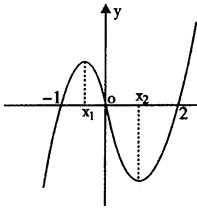
如下图是函数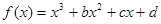 的大致图象,则
的大致图象,则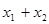 = ( )
= ( )
A.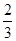 | B.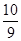 | C.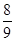 | D.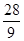 |
A
解析试题分析:∵f(x)=x3+bx2+cx+d,由图象知,-1+b-c+d=0,0+0+0+d=0,
8+4b+2c+d=0,∴d=0,b=-1,c=-2
∴f′ (x)=3x2+2bx+c=3x2-2x-2. 由题意有 x1 和 x2 是函数f(x)的极值,
故有 x1 和 x2 是 f′ (x)=0的根,∴x1+x2=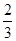
故选A。
考点:本题主要考查一元二次方程的根的分布与系数的关系;函数在某点取得极值的条件.
点评:基础题,利用数形结合思想,通过观察图象确定得到b,c,d的值是解题的关键。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
函数 在
在 处的切线方程是
处的切线方程是
A. | B. |
C. | D. |
如果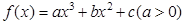 导函数图像的顶点坐标为
导函数图像的顶点坐标为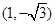 ,那么曲线
,那么曲线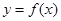 上任一点的切线的倾斜角
上任一点的切线的倾斜角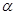 的取值范围是( )
的取值范围是( )
A.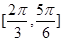 | B.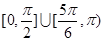 |
C.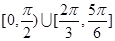 | D.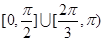 |
若曲线 在点
在点 处的切线与两个坐标围成的三角形的面积为18,则
处的切线与两个坐标围成的三角形的面积为18,则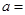 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
若函数 的导函数
的导函数 ,则函数
,则函数 的单调递减区间是( )
的单调递减区间是( )
A.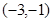 | B.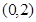 | C. | D.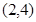 |
设函数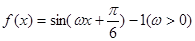 的导函数
的导函数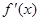 的最大值为3,则
的最大值为3,则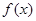 的图象的一条对称轴的方程是( )
的图象的一条对称轴的方程是( )
A.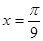 | B.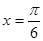 | C.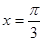 | D.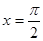 |
曲线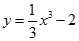 在点(
在点(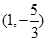 处切线的倾斜角为( )
处切线的倾斜角为( )
A.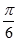 | B.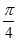 | C.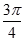 | D.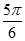 |
 在定义域内可导,
在定义域内可导, 的图象如图所示,则导函数
的图象如图所示,则导函数 可能为
可能为