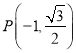题目内容
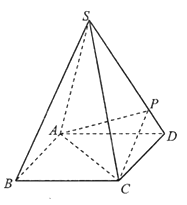
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.
(1)求证:![]() ;
;
(2)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)在(2)的条件下,侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() .若存在,求
.若存在,求![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
【答案】(1)见证明;(2) ![]() (3)见解析
(3)见解析
【解析】
(1)先证明![]() 平面
平面![]() ,即可得到
,即可得到![]() ;
;
(2)由题设知,连![]() ,设
,设![]() 交于
交于![]() 于
于![]() ,由题意知
,由题意知![]() 平面
平面![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立空间直角坐标系,分别求出平面
轴正方向,建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的一个法向量,求法向量的夹角余弦值,即可求出结果;
的一个法向量,求法向量的夹角余弦值,即可求出结果;
(3)要使![]() 平面
平面![]() ,只需
,只需![]() 与平面的法向量垂直即可,结合(2)中求出的平面
与平面的法向量垂直即可,结合(2)中求出的平面![]() 的一个法向量,即可求解.
的一个法向量,即可求解.
(1)连![]() 交
交![]() 于
于![]() ,由题意
,由题意![]() .
.
在正方形![]() 中,
中,![]() ,
,
所以![]() 平面
平面![]() ,得
,得![]()
(2)由题设知,连![]() ,设
,设![]() 交于
交于![]() 于
于![]() ,由题意知
,由题意知![]() 平面
平面![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立坐标系
轴正方向,建立坐标系![]() 如图.
如图.

设底面边长为![]() ,则高
,则高![]() .
.
则![]() ,
,![]() ,
,![]()
又![]() 平面
平面![]() ,
,
则平面![]() 的一个法向量
的一个法向量![]() ,
,
平面![]() 的一个法向量
的一个法向量![]() ,
,
则![]() ,
,
又二面角![]() 为锐角,则二面角
为锐角,则二面角![]() 为
为![]() ;
;
(3)在棱![]() 上存在一点
上存在一点![]() 使
使![]() 平面
平面![]() .由(2)知
.由(2)知![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
且![]() ,
,![]()
设![]() ,
,![]()
则![]()
![]()
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
则![]() .
.
即当![]() 时,
时,![]()
而![]() 不在平面
不在平面![]() 内,故
内,故![]() 平面
平面![]() .
.

【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
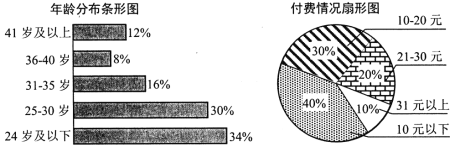
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
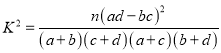 .
.