题目内容
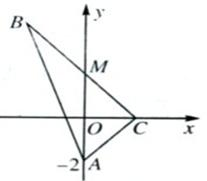 如图所示,在△ABC中,
如图所示,在△ABC中,| CA |
| CB |
| OA |
| AM |
| 1 |
| 2 |
| AB |
| AC |
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点F(0,-
| 1 |
| 4 |
| FH |
| 1 |
| 2 |
| HG |
分析:(Ⅰ)先设B(x,y),C(a,0),M(0,b),a≠0,根据
⊥
,得出∠ACB=90°,于是a2=2b,再结合M在y轴上,及题中向量关系得出M是BC的中点,x,y的关系式即为B的轨迹E的方程;
(Ⅱ)设满足条件的直线l的方程,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量关系式即可求得k值,从而解决问题.
| CA |
| CB |
(Ⅱ)设满足条件的直线l的方程,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量关系式即可求得k值,从而解决问题.
解答:解:(Ⅰ)设B(x,y),C(a,0),M(0,b),a≠0,∵
⊥
,即∠ACB=90°∴
•
=-1,
于是a2=2b①M在y轴上,且
=
(
+
),∴M是BC的中点,可得
∴
②
把②代入①得y=x2(x≠0),所以B的轨迹E的方程为y=x2(x≠0)(6分)
(Ⅱ)点F(0,-
),设满足条件的直线l的方程为y=kx-
,H(x1,y1),G(x2,y2)
由
得x2-kx+
=0,△=k2-1>0,∴k2>1,
∵
=
,
∴(x1,y1+
)=
(x2-x1,y1-y2),
∴x1=
x2-
x1,
∴3x1=x2,
∵x1+x2=k,x1x2=
,
∴k=±
(13分)
直线l的斜率:k=±
.
| CA |
| CB |
| 2 |
| a |
| b |
| -a |
于是a2=2b①M在y轴上,且
| AM |
| 1 |
| 2 |
| AB |
| AC |
|
|
把②代入①得y=x2(x≠0),所以B的轨迹E的方程为y=x2(x≠0)(6分)
(Ⅱ)点F(0,-
| 1 |
| 4 |
| 1 |
| 4 |
由
|
| 1 |
| 4 |
∵
| FH |
| 1 |
| 2 |
| HG |
∴(x1,y1+
| 1 |
| 4 |
| 1 |
| 2 |
∴x1=
| 1 |
| 2 |
| 1 |
| 2 |
∴3x1=x2,
∵x1+x2=k,x1x2=
| 1 |
| 4 |
∴k=±
2
| ||
| 3 |
直线l的斜率:k=±
2
| ||
| 3 |
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,提高解题能力和解题时技巧,注意合理地进行等价转化.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
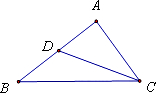 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
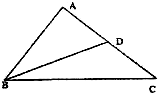 如图所示,在△ABC,已知
如图所示,在△ABC,已知 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD= 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=