题目内容
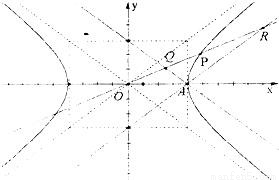
设双曲线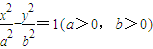 的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点.(如图)
的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点.(如图)(1)证明:无论P点在什么位置,总有
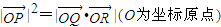 ;
;(2)若以OP为边长的正方形面积等于双曲线实、虚轴围成的矩形面积,求双曲线离心率的取值范围.
【答案】分析:(1)先求出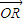 、
、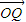 的坐标,计算
的坐标,计算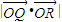 的值,把双曲线方程与OP方程联立解得
的值,把双曲线方程与OP方程联立解得 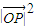 ,比较可得
,比较可得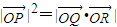 .
.
(2)由条件得: ,根据k2>0,得到b>
,根据k2>0,得到b>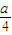 ,计算e=
,计算e=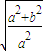 的范围.
的范围.
解答:解:(1)设OP的方程为 y=kx,AR的方程为 y=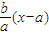 ,
,
解得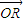 =
=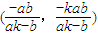 ,同理可得
,同理可得 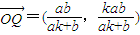 .
.
∴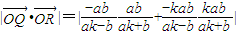 =
=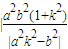 .
.
设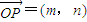 ,则由双曲线方程与OP方程联立解得:
,则由双曲线方程与OP方程联立解得:
∴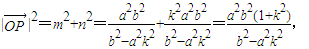
∵点P在双曲线上,∴b2-a2k2>0,无论点P在什么位置,总有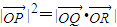 .
.
(2)由条件得: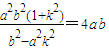 ,即
,即 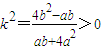 ,
,
∴4b>a,∴e= =
=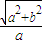 >
> =
=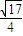 ,即 e>
,即 e>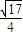 .
.
点评:本题考查两个向量的数量积,双曲线的标准方程,以及双曲线的简单性质的应用,式子的变形、化简是解题的难点.
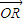 、
、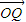 的坐标,计算
的坐标,计算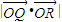 的值,把双曲线方程与OP方程联立解得
的值,把双曲线方程与OP方程联立解得 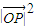 ,比较可得
,比较可得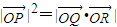 .
.(2)由条件得:
 ,根据k2>0,得到b>
,根据k2>0,得到b>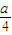 ,计算e=
,计算e=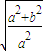 的范围.
的范围.解答:解:(1)设OP的方程为 y=kx,AR的方程为 y=
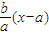 ,
,解得
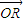 =
=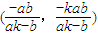 ,同理可得
,同理可得 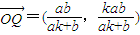 .
.∴
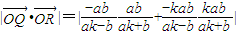 =
=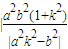 .
.设
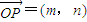 ,则由双曲线方程与OP方程联立解得:
,则由双曲线方程与OP方程联立解得:
∴
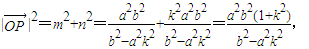
∵点P在双曲线上,∴b2-a2k2>0,无论点P在什么位置,总有
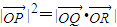 .
.(2)由条件得:
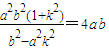 ,即
,即 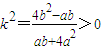 ,
,∴4b>a,∴e=
 =
=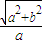 >
> =
=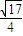 ,即 e>
,即 e>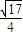 .
.点评:本题考查两个向量的数量积,双曲线的标准方程,以及双曲线的简单性质的应用,式子的变形、化简是解题的难点.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
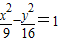 的右顶点为A,右焦点为F,此双曲线的渐近线方程为 ;过点F平行双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为 .
的右顶点为A,右焦点为F,此双曲线的渐近线方程为 ;过点F平行双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为 .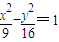 的右顶点为A,右焦点为F.过点F且与双曲线的一条渐近线平行的直线与另一条渐近线交于点B,则△AFB的面积为 .
的右顶点为A,右焦点为F.过点F且与双曲线的一条渐近线平行的直线与另一条渐近线交于点B,则△AFB的面积为 .