题目内容
设双曲线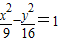
的右顶点为A，右焦点为F，此双曲线的渐近线方程为 ；过点F平行双曲线的一条渐近线的直线与双曲线交于点B，则△AFB的面积为 ．
【答案】分析：根据题意，由双曲线的方程可得a、b的值，进而可得c的值，可以确定双曲线的渐近线方程，A、F的坐标，设BF的方程为y=
（x-5），代入双曲线方程解得B的坐标，计算可得答案．
解答：解：根据题意，得a2=9，b2=16，
∴c=5，且A（3，0），F（5，0），
∵双曲线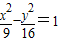
的渐近线方程为y=±
x；
不妨设BF的方程为y=
（x-5），
代入双曲线方程解得：B（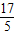
，-
）．
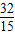∴S△AFB=
|AF|•|yB|=
•2•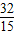
=
．
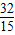故答案为：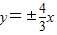
，
．
点评：本题考查双曲线方程的运用，注意关键在与求出B的坐标；解此类面积的题目时，注意要使三角形的底或高与坐标轴平行或重合，以简化计算．
（x-5），代入双曲线方程解得B的坐标，计算可得答案．解答：解：根据题意，得a2=9，b2=16，
∴c=5，且A（3，0），F（5，0），
∵双曲线
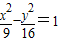的渐近线方程为y=±x；不妨设BF的方程为y=
（x-5），代入双曲线方程解得：B（
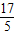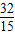，-）．∴S△AFB=
|AF|•|yB|=•2•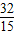=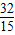．故答案为：
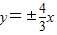，．点评：本题考查双曲线方程的运用，注意关键在与求出B的坐标；解此类面积的题目时，注意要使三角形的底或高与坐标轴平行或重合，以简化计算．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
的右顶点为A，右焦点为F．过点F平行双曲线的一条渐近线的直线与双曲线交于点B，则△AFB的面积为 ．
的右顶点为A，右焦点为F，过点F平行双曲线的一条渐近线的直线与双曲线交于点B，则△AFB的面积为 。
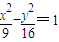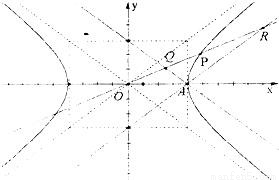
的右顶点为A，右焦点为F．过点F且与双曲线的一条渐近线平行的直线与另一条渐近线交于点B，则△AFB的面积为 ．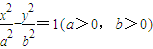
的右顶点为A，P是双曲线上异于顶点的一个动点，从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点．（如图）
；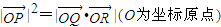