题目内容
直线y=x+b与曲线x=
有且仅有一个公共点,则b的取值范围是( )
| 1-y2 |
A、|b|=
| ||
B、-1<b≤1或b=-
| ||
C、-1≤b≤
| ||
D、
|
分析:把曲线方程整理后可知其图象为半圆,进而画出图象来,要使直线与曲线有且仅有一个交点,那么很容易从图上看出其三个极端情况分别是:直线在第四象限与曲线相切,交曲线于(0,-1)和另一个点,及与曲线交于点(0,1),分别求出b,则b的范围可得.
解答: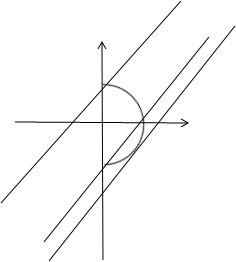 解:x=
解:x=
化简得x2+y2=1
注意到x≥0
所以这个曲线应该是半径为1,圆心是(0,0)的半圆,且其图象只在一四象限.
这样很容易画出图来,这样因为直线与其只有一个交点,
那么很容易从图上看出其三个极端情况分别是:
直线在第四象限与曲线相切,
交曲线于(0,-1)和另一个点,
及与曲线交于点(0,1).
分别算出三个情况的B值是:-
,-1,1.
因为B就是直线在Y轴上的截距了,
所以看图很容易得到B的范围是:-1<b≤1或b=-
故选B
 解:x=
解:x=| 1-y2 |
注意到x≥0
所以这个曲线应该是半径为1,圆心是(0,0)的半圆,且其图象只在一四象限.
这样很容易画出图来,这样因为直线与其只有一个交点,
那么很容易从图上看出其三个极端情况分别是:
直线在第四象限与曲线相切,
交曲线于(0,-1)和另一个点,
及与曲线交于点(0,1).
分别算出三个情况的B值是:-
| 2 |
因为B就是直线在Y轴上的截距了,
所以看图很容易得到B的范围是:-1<b≤1或b=-
| 2 |
故选B
点评:本题主要考查了直线与圆相交的性质.对于此类问题除了用联立方程转化为方程的根的问题之外,也可用数形结合的方法较为直观.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
若直线y=x-b与曲线
(θ∈[0,2π))有两个不同的公共点,则实数b的取值范围为( ).
|
A、(2-
| ||||
B、[2-
| ||||
C、(-∞,2-
| ||||
D、(2-
|
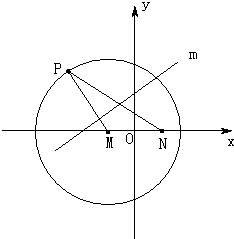 如图,已知
如图,已知