题目内容
14.已知数列{bn}的前n项和为Sn,b1=1,且点(n.Sn+n+2)在函数y=2x+1的图象上,若数列{an}满足a1=1,an=bn($\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$)(n≥2,n∈N*).(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)(i)求证:$\frac{{a}_{n}+1}{{a}_{n+1}}$=$\frac{{b}_{n}}{{b}_{n+1}}$(n≥2,n∈N*);
(ii)求证:(1+$\frac{1}{{a}_{1}}$)(1+$\frac{1}{{a}_{2}}$)(1+$\frac{1}{{a}_{3}}$)…(1+$\frac{1}{{a}_{n}}$)<$\frac{10}{3}$.
分析 (Ⅰ)由题意可得Sn=2n+1-n-2,b1=1,再由前n项和与通项的关系求得bn=2n-1;
(Ⅱ)(i)根据an=bn($\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$)可得$\frac{{a}_{n}}{{b}_{n}}$,从而有$\frac{{a}_{n+1}}{{b}_{n+1}}$,所以$\frac{{a}_{n+1}}{{b}_{n+1}}$-$\frac{{a}_{n}}{{b}_{n}}$=$\frac{1}{{b}_{n}}$,变形可得结论;
(ii)注意讨论,当n=1时成立,当n≥2时,由(Ⅱ)(i)知(1+$\frac{1}{{a}_{1}}$)(1+$\frac{1}{{a}_{2}}$)(1+$\frac{1}{{a}_{3}}$)…(1+$\frac{1}{{a}_{n}}$)
=$\frac{1+{a}_{1}}{{a}_{1}{a}_{2}}$•$\frac{1+{a}_{2}}{{a}_{3}}$•$\frac{1+{a}_{3}}{{a}_{4}}$•…•$\frac{1+{a}_{n}}{{a}_{n+1}}$•an+1=$\frac{2}{3}$•$\frac{{b}_{2}}{{b}_{3}}$•$\frac{{b}_{3}}{{b}_{4}}$•$\frac{{b}_{4}}{{b}_{5}}$•…•$\frac{{b}_{n}}{{b}_{n+1}}$•an+1=$\frac{2}{3}$•$\frac{{b}_{2}}{{b}_{n+1}}$•an+1=2•$\frac{{a}_{n}+1}{{a}_{n+1}}$═2($\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$+$\frac{1}{{b}_{n}}$)=2(1+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$),再放缩求解即可得证.
解答 解:(Ⅰ)点(n.Sn+n+2)在函数y=2x+1的图象上,
∴Sn+n+2=2n+1,则Sn=2n+1-n-2,b1=1,
n≥2时,Sn-1=2n-n-1,∴Sn-Sn-1=2n-1,
即bn=2n-1(n≥2),b1=1满足该式,故bn=2n-1.
(Ⅱ)(i)证明:∵an=bn($\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$)(n≥2,n∈N*),
∴$\frac{{a}_{n}}{{b}_{n}}$=$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$,$\frac{{a}_{n+1}}{{b}_{n+1}}$=$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$+$\frac{1}{{b}_{n}}$,
∴$\frac{{a}_{n+1}}{{b}_{n+1}}$-$\frac{{a}_{n}}{{b}_{n}}$=$\frac{1}{{b}_{n}}$,从而$\frac{{a}_{n+1}}{{b}_{n+1}}$=$\frac{{a}_{n}}{{b}_{n}}$+$\frac{1}{{b}_{n}}$=$\frac{{a}_{n}+1}{{b}_{n}}$,
∴$\frac{{a}_{n}+1}{{a}_{n+1}}$=$\frac{{b}_{n}}{{b}_{n+1}}$;
(ii)证明:b1=1,b2=3,a1=1,a2=3,
当n=1时,左边=1+$\frac{1}{{a}_{1}}$=2<$\frac{10}{3}$=右边.
当n≥2时,由(Ⅱ)(i)知(1+$\frac{1}{{a}_{1}}$)(1+$\frac{1}{{a}_{2}}$)(1+$\frac{1}{{a}_{3}}$)…(1+$\frac{1}{{a}_{n}}$)
=$\frac{1+{a}_{1}}{{a}_{1}}$•$\frac{1+{a}_{2}}{{a}_{2}}$•$\frac{1+{a}_{3}}{{a}_{3}}$•…•$\frac{1+{a}_{n}}{{a}_{n}}$
=$\frac{1+{a}_{1}}{{a}_{1}{a}_{2}}$•$\frac{1+{a}_{2}}{{a}_{3}}$•$\frac{1+{a}_{3}}{{a}_{4}}$•…•$\frac{1+{a}_{n}}{{a}_{n+1}}$•an+1
=$\frac{2}{3}$•$\frac{{b}_{2}}{{b}_{3}}$•$\frac{{b}_{3}}{{b}_{4}}$•$\frac{{b}_{4}}{{b}_{5}}$•…•$\frac{{b}_{n}}{{b}_{n+1}}$•an+1
=$\frac{2}{3}$•$\frac{{b}_{2}}{{b}_{n+1}}$•an+1=2•$\frac{{a}_{n}+1}{{a}_{n+1}}$═2($\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$+$\frac{1}{{b}_{n}}$),
而$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$+$\frac{1}{{b}_{n}}$=1+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$,
当k≥2时,$\frac{1}{{2}^{k}-1}$=$\frac{{2}^{k+1}-1}{({2}^{k}-1)({2}^{k+1}-1)}$<$\frac{{2}^{k+1}}{({2}^{k}-1)({2}^{k+1}-1)}$=2($\frac{1}{{2}^{k}-1}$-$\frac{1}{{2}^{k+1}-1}$),
∴1+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$<1+2($\frac{1}{{2}^{2}-1}$-$\frac{1}{{2}^{3}-1}$+$\frac{1}{{2}^{3}-1}$-$\frac{1}{{2}^{4}-1}$+…+$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$)
=1+2($\frac{1}{3}$-$\frac{1}{{2}^{n+1}-1}$)<1+$\frac{2}{3}$=$\frac{5}{3}$,
∴(1+$\frac{1}{{a}_{1}}$)(1+$\frac{1}{{a}_{2}}$)(1+$\frac{1}{{a}_{3}}$)…(1+$\frac{1}{{a}_{n}}$)<$\frac{10}{3}$.
点评 本题主要考查数列与函数,不等式的综合运用,同时考查数列前n项和与通项的关系以及放缩法,裂项法等.属于难题.

| A. | 命题“若x2<1,则-1<x<1”的逆否命题是“若x≥1或x≤-1,则x2≥1” | |
| B. | “am2<bm2”是“a<b”的充分不必要条件 | |
| C. | 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 | |
| D. | 命题p:存在x0∈R,使得${{x}_{0}}^{2}$+x0+1<0,则¬p:任意x∈R,都有x2+x+1≥0 |
| A. | 0<k<8,C1与C2的实轴长相等 | B. | k<6,C1与C2的实轴长相等 | ||
| C. | 0<k<8,C1与C2的焦距相等 | D. | k<6,C1与C2的焦距相等 |
| A. | x2+(y-a)2=a2 | B. | y2=2ax | C. | (x-a)2+y2=a2 | D. | x2=2ay |
| A. | $\frac{π}{4}$,$\frac{3π}{4}$ | B. | $\frac{3π}{4}$,$\frac{5π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{5π}{4}$,$\frac{7π}{4}$ |
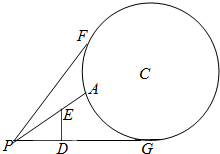 如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.
如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.