题目内容
4．下列命题错误的是（ ）| A． | 命题“若x2＜1，则-1＜x＜1”的逆否命题是“若x≥1或x≤-1，则x2≥1” | |
| B． | “am2＜bm2”是“a＜b”的充分不必要条件 | |
| C． | 命题“p或q”为真命题，则命题“p”和命题“q”均为真命题 | |
| D． | 命题p：存在x0∈R，使得${{x}_{0}}^{2}$+x0+1＜0，则￢p：任意x∈R，都有x2+x+1≥0 |
分析 A中逆否命题应先逆得逆命题：条件结论互换；再求否命题：条件，结论都否定；
B中am2＜bm2能推出a＜b，但a＜b不能推出am2＜bm2，当m2=0时不成立；
C中p或q为真，则只要有一个为真就可以；
D中存在命题的否定，应把存在改为任意，再否定结论．
解答 解：A中逆否命题应先逆得逆命题：条件结论互换；再求否命题：条件，结论都否定；故正确；
B中am2＜bm2能推出a＜b，但a＜b不能推出am2＜bm2，当m2=0时不成立，故正确；
C中p或q为真，则只要有一个为真就可以，故错误；
D中存在命题的否定，应把存在改为任意，再否定结论，命题p：存在x0∈R，使得${{x}_{0}}^{2}$+x0+1＜0，则￢p：任意x∈R，都有x2+x+1≥0，故正确．
故选C．
点评 考查了四中命题，属于基础题型，应牢记．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
14．sin160°cos10°+cos20°sin10°=（ ）
| A． | $-\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |
15．经过双曲线上任一点M作平行于实轴的直线，与渐近线交于P、Q两点，则|MP|•|MQ|为定值，其值为（ ）
| A． | a2 | B． | b2 | C． | c2 | D． | ab |
12．已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{{m}^{2}}$=1，焦点在x轴上，则m的取值范围是（ ）
| A． | -4≤m≤4 | B． | -4＜m＜4且m≠0 | C． | m＞4或m＜-4 | D． | 0＜m＜4 |
9．函数y=x3-3x2-9x+5的极值情况是（ ）
| A． | 在x=-1处取得极大值，但没有最小值 | |
| B． | 在x=3处取得极小值，但没有最大值 | |
| C． | 在x=-1处取得极大值，在x=3处取得极小值 | |
| D． | 既无极大值也无极小值 |
16．
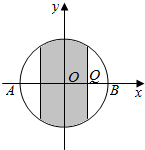如图所示，在单位圆O的某一直径AB上随机地取一点Q，则过点Q且与该直径垂直的
弦的长度不超过1的概率（ ）
如图所示，在单位圆O的某一直径AB上随机地取一点Q，则过点Q且与该直径垂直的弦的长度不超过1的概率（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | 1-$\frac{\sqrt{3}}{2}$ | D． | 1-$\frac{\sqrt{2}}{2}$ |
13．为了得到函数y=sin3x+cos3x图象，可将函数$y=\sqrt{2}sin3x$图象（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{12}$个单位 | ||
| C． | 向右平移$\frac{π}{4}$个单位 | D． | 向左平移$\frac{π}{4}$个单位 |