题目内容
3．在${（\sqrt{x}+\frac{2}{x^2}）^n}（n∈{N^*}）$的展开式中，若第五项的系数与第三项的系数之比为56：3，则展开式中的常数项是（ ）| A． | 第2项 | B． | 第3项 | C． | 第4项 | D． | 第5项 |
分析 在展开式的通项中，令x=1得出第5项的系数与第3项的系数表达式，由已知，求出n，再在通项中令x得指数为0，确定常数项．
解答 解：展开式的通项为Tr+1=${C}_{n}^{r}•{2}^{r}•{x}^{\frac{n-5r}{2}}$
第5项的系数为${C}_{n}^{4}$•24，第3项的系数为${C}_{n}^{2}$•22，
由已知，得出${C}_{n}^{4}$•24：${C}_{n}^{2}$•22=56：3，解得n=10
令10-5r=0，可得r=2时，取到常数项，
故选：B．
点评 本题考查二项式定理的应用：求指定的项．牢记公式是基础，方程思想是关键．
练习册系列答案
相关题目
13．正实数数列{an}满足：a1=1，a9=7，且an+1=$\frac{（{a}_{n}+1）^2-（{a}_{n-1}+1）}{{a}_{n-1}+1}$（n∈N+，n≥2）则a5=（ ）
| A． | 4 | B． | 3 | C． | 16 | D． | 9 |
14．若$z=\frac{i}{1+2i}$，i为虚数单位，则|z|=（ ）
| A． | $\sqrt{5}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
11．若函数$f（x）=2sin（ωx+\frac{π}{3}）$，且f（α）=-2，f（β）=0，|α-β|的最小值是$\frac{π}{2}$，则f（x）的单调递增区间是（ ）
| A． | $[kπ-\frac{5π}{12}，kπ+\frac{π}{12}]\;\;（k∈Z）$ | B． | $[kπ-\frac{π}{3}，kπ+\frac{π}{6}]\;\;（k∈Z）$ | ||
| C． | $[2kπ-\frac{2π}{3}，2kπ+\frac{π}{3}]\;\;（k∈Z）$ | D． | $[2kπ-\frac{5π}{6}，2kπ+\frac{π}{6}]\;（\;k∈Z）$ |
8．已知$（{2+\sqrt{3}i}）•z=-2\sqrt{3}i$（i是虚数单位），那么复数z对应的点位于复平面内的（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
15．程序框图如图所示，若其输出结果是30，则判断框中填写的是（ ）
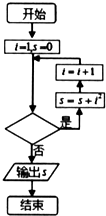
| A． | i＜7？ | B． | i＜5？ | C． | i＞7？ | D． | i＞5？ |
12．已知A，B，C为不共线的三点，则“$\overrightarrow{AB}•\overrightarrow{CA}＞0$”是“△ABC是钝角三角形”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |