题目内容
以下四个关于圆锥曲线的命题中:①设A、B为两个定点,k为非零常数,
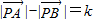 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;②平面内到两定点距离之和等于常数的点的轨迹是椭圆
③若方程
 表示焦点在x轴上的椭圆,则1<t<
表示焦点在x轴上的椭圆,则1<t<
④双曲线
 有相同的焦点.
有相同的焦点.其中真命题的序号为 (写出所有真命题的序号)
【答案】分析:①不正确.若动点P的轨迹为双曲线,则|k|要小于A、B为两个定点间的距离;②不正确,若平面内到两定点距离之和等于常数,常数为大于两个点的距离;③正确,若方程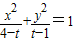 表示焦点在x轴上的椭圆,则4-t>t-1>0,④正确,焦点在x轴上,焦点坐标为(±
表示焦点在x轴上的椭圆,则4-t>t-1>0,④正确,焦点在x轴上,焦点坐标为(± ,0).
,0).
解答:解:①不正确.若动点P的轨迹为双曲线,则|k|要小于A、B为两个定点间的距离.当|k|大于A、B为两个定点间的距离时动点P的轨迹不是双曲线.
②不正确,若平面内到两定点距离之和等于常数,常数为两个点的距离的轨迹是两点的垂直平方线,而不是椭圆;
③正确,若方程 表示焦点在x轴上的椭圆,则4-t>t-1>0,解得1<t<
表示焦点在x轴上的椭圆,则4-t>t-1>0,解得1<t< ;
;
④正确,双曲线 有相同的焦点,焦点在x轴上,焦点坐标为(±
有相同的焦点,焦点在x轴上,焦点坐标为(±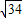 ,0);
,0);
故答案为:③、④
点评:本题主要考查了圆锥曲线的共同特征,同时考查了椭圆与双曲线的性质,考查的知识点较多,属于中档题.
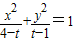 表示焦点在x轴上的椭圆,则4-t>t-1>0,④正确,焦点在x轴上,焦点坐标为(±
表示焦点在x轴上的椭圆,则4-t>t-1>0,④正确,焦点在x轴上,焦点坐标为(± ,0).
,0).解答:解:①不正确.若动点P的轨迹为双曲线,则|k|要小于A、B为两个定点间的距离.当|k|大于A、B为两个定点间的距离时动点P的轨迹不是双曲线.
②不正确,若平面内到两定点距离之和等于常数,常数为两个点的距离的轨迹是两点的垂直平方线,而不是椭圆;
③正确,若方程
 表示焦点在x轴上的椭圆,则4-t>t-1>0,解得1<t<
表示焦点在x轴上的椭圆,则4-t>t-1>0,解得1<t< ;
;④正确,双曲线
 有相同的焦点,焦点在x轴上,焦点坐标为(±
有相同的焦点,焦点在x轴上,焦点坐标为(±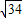 ,0);
,0);故答案为:③、④
点评:本题主要考查了圆锥曲线的共同特征,同时考查了椭圆与双曲线的性质,考查的知识点较多,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目