题目内容
(本小题满分10分)△ABC中,内角A,B,C的对边分别为a,b,c,已知a,b,c成等比数列,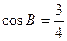
(Ⅰ)求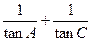 的值; (Ⅱ)设
的值; (Ⅱ)设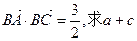 的值
的值
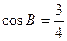
(Ⅰ)求
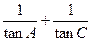 的值; (Ⅱ)设
的值; (Ⅱ)设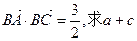 的值
的值(Ⅰ)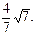 (Ⅱ)
(Ⅱ)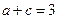
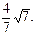 (Ⅱ)
(Ⅱ)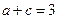
(Ⅰ)由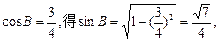
由b2=ac及正弦定理得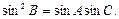
于是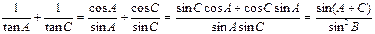
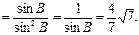
(Ⅱ)由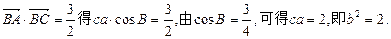
由余弦定理 b2=a2+c2-2ac+cosB 得a2+c2=b2+2ac·cosB=5.
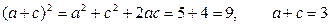
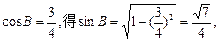
由b2=ac及正弦定理得
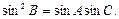
于是
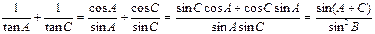
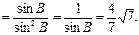
(Ⅱ)由
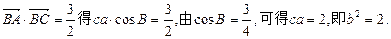
由余弦定理 b2=a2+c2-2ac+cosB 得a2+c2=b2+2ac·cosB=5.
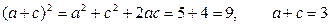

练习册系列答案
相关题目
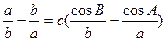
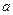 、
、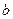 、
、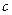 ,且
,且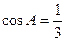 .
.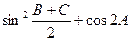 的值;
的值;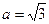 ,求
,求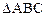 面积的最大值.
面积的最大值.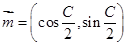 ,
, ,且
,且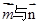 的夹角是
的夹角是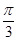
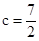 ,三角形ABC的面积
,三角形ABC的面积 ,求a+b.
,求a+b.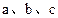 是角
是角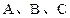 所对的边,且满足
所对的边,且满足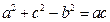 .
.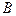 的大小;
的大小;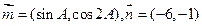 ,求
,求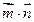 的最小值.
的最小值. 在数学研究性学习活动中,某小组要测量河对面
在数学研究性学习活动中,某小组要测量河对面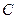 和
和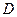 两个建筑物的距离,作图如下,所测得的数据为
两个建筑物的距离,作图如下,所测得的数据为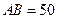 米,
米,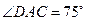 ,
,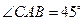 ,
,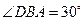 ,
,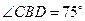 ,请你帮他们计算一下,河对岸建筑物
,请你帮他们计算一下,河对岸建筑物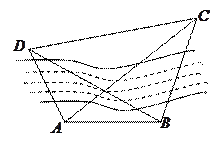
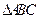 中,角
中,角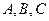 所对的边分别为
所对的边分别为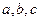 且
且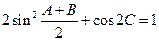 (1)求角的
(1)求角的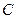 大小(2)若向量
大小(2)若向量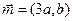 ,向量
,向量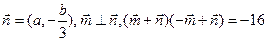 ,求
,求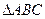 中,内角
中,内角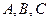 的对边分别为
的对边分别为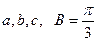 ,
,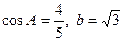 。(1)求边
。(1)求边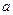 的大小;(2)求
的大小;(2)求
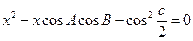 有一个根为1,则
有一个根为1,则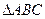 一定是( )
一定是( )