题目内容
(本小题12分)
已知函数
(1)求函数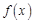 的单调区间和极值;
的单调区间和极值;
(2)已知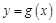 的图象与函数
的图象与函数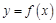 的图象关于直线
的图象关于直线 对称,证明:当
对称,证明:当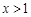 时,
时,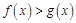 ;
;
(3)如果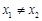 且
且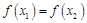 ,证明:
,证明: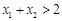
(1)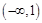 增,
增,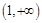 减
减
(2) (3)见解析
解析

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
题目内容
(本小题12分)
已知函数
(1)求函数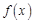 的单调区间和极值;
的单调区间和极值;
(2)已知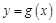 的图象与函数
的图象与函数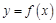 的图象关于直线
的图象关于直线 对称,证明:当
对称,证明:当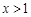 时,
时,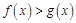 ;
;
(3)如果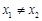 且
且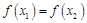 ,证明:
,证明: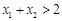
(1)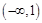 增,
增,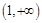 减
减
(2) (3)见解析
解析

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案