题目内容
12.设A={递增等比数列的公比},B={递减等比数列的公比},则A∪B=( )| A. | (-∞,+∞) | B. | (1,+∞) | C. | (0,1)∪(1,+∞) | D. | ∅ |
分析 当首项是正数时:递增等比数列的公比q>1,递减等边数列的公比0<q<1.
当首项是负数时:递增等比数列的公比0<q<1,递减等边数列的公比q>1.
解答 解:A={递增等比数列的公比},B={递减等比数列的公比}.
①当首项是正数时:A={q|q>1},B={q|0<q<1},
则A∪B=(0,1)∪(1,+∞);
②当首项是负数时:A={q|0<q<1},B={q|q>1},
则A∪B=(0,1)∪(1,+∞);
综上所述:A∪B=(0,1)∪(1,+∞).
故选:C.
点评 本题考查了等比数列的单调性、分类讨论等基础知识与基本方法,属于基础题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
4.阅读下面的流程图,若输入a=5,b=-1,则输出的a值为( )
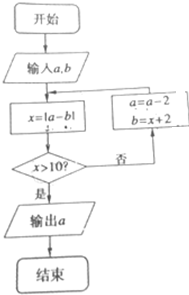

| A. | 16 | B. | 10 | C. | -3 | D. | -5 |