题目内容
17.将一颗骰子投掷两次得到的点数分别为a,b,则函数f(x)=ax3+bx2+x存在极值的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{5}{9}$ | C. | $\frac{7}{12}$ | D. | $\frac{2}{3}$ |
分析 利用古典概型概率计算公式,先计算总的基本事件数,再根据要取得极值,导函数为0的方程恰有两个不同的解,利用判别式,即可求得结论.
解答 解:f(x)=ax3+bx2+x,
∴f′(x)=3ax2+2bx+1,
∵f(x)=ax3+bx2+x存在极值,
∴f′(x)=3ax2+2bx+1=0恰有两个不同的解,
∴△=4b2-12a>0,即b2>3a
设一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个,
其中b2>3a的有(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,4),(4,5),(4,6),(5,4),(5,5),(5,6),(6,5),(6,6)共20个,
则函数f(x)=ax3+bx2+x存在极值的概率为$\frac{20}{36}$=$\frac{5}{9}$.
故选:B.
点评 本题考查了古典概型概率的计算方法,导数和极值的关系,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
7.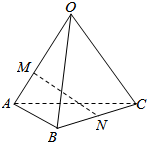 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )
 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )| A. | $\frac{1}{2}\vec a-\frac{2}{3}\vec b+\frac{1}{2}\vec c$ | B. | $-\frac{2}{3}\vec a+\frac{1}{2}\vec b+\frac{1}{2}\vec c$ | C. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b-\frac{1}{2}\vec c$ | D. | $\frac{2}{3}\vec a+\frac{2}{3}\vec b-\frac{1}{2}\vec c$ |
8.顶点在x轴上,两顶点间的距离为4,离心率e=$\frac{\sqrt{5}}{2}$的双曲线与直线y=kx(k∈R)无交点,则实数k的取值范围为( )
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | (-∞,-$\frac{1}{2}$]∪[$\frac{1}{2}$,∞) | C. | (-$\frac{1}{2}$,$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
2.甲乙两人向某个目标射击,他们每次击中目标的概率如下表:
(Ⅰ)若两人同时向目标射击一次,求目标被击中的概率;
(Ⅱ)若由甲开始两人轮流向目标射击,击中目标就停止,现在共有5发子弹,写出使用子弹数?分布列,求?的期望(均值).
| 第一次 | 第二次 | 第三次 | |
| 甲 | 0.4 | 0.6 | 0.8 |
| 乙 | 0.5 | 0.6 | 0.9 |
(Ⅱ)若由甲开始两人轮流向目标射击,击中目标就停止,现在共有5发子弹,写出使用子弹数?分布列,求?的期望(均值).