题目内容
(本小题满分1 3分)
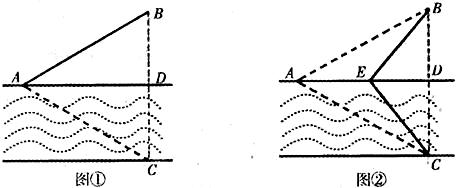
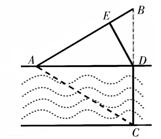
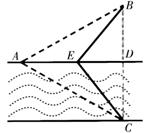
如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现
决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤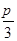 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
【答案】
解:(Ⅰ)由已知可得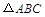 为等边三角形.
为等边三角形.
因为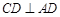 ,所以水下电缆的最短线路为
,所以水下电缆的最短线路为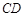 .
.
过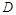 作
作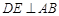 于E,可知地下电缆的最短线路为
于E,可知地下电缆的最短线路为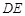 、
、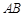 . ······· 3分
. ······· 3分
又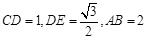 ,
,
故该方案的总费用为
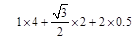
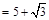 (万元) …………6分
(万元) …………6分
(Ⅱ)因为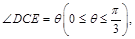
所以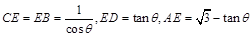 .·············· 7分
.·············· 7分
则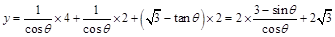 ,
········ 9分
,
········ 9分
令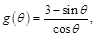 则
则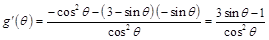 , ···· 10分
, ···· 10分
因为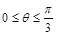 ,所以
,所以 ,
,
记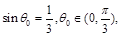
当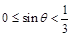 ,即
,即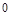 ≤
≤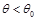 时,
时,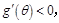
当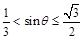 ,即
,即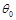 <
<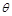 ≤
≤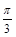 时,
时,
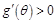 ,
,
所以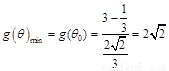 ,从而
,从而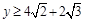 ,·········· 12分
,·········· 12分
此时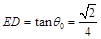 ,
,
因此施工总费用的最小值为(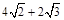 )万元,其中
)万元,其中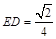 . ··· 13分
. ··· 13分
【解析】略

练习册系列答案
相关题目
 (x2—600)万元作为技改费用,投入50万元作为固定宣传费用,投入
(x2—600)万元作为技改费用,投入50万元作为固定宣传费用,投入 x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.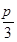 ,AC=4
,AC=4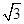 ,D为BC边上一点.
,D为BC边上一点.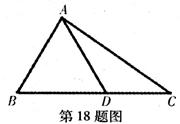
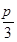 ,S△ABC=6
,S△ABC=6